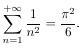Portrait de Denis Favennec

J’ai rencontré Denis à l’oral de l’agrégation de mathématiques, nous faisions tous les deux partie du jury. Je l’ai plus particulièrement rencontré un jour pendant la pause du déjeuner, où il avait proposé aux membres du jury qui le souhaitaient, une conférence sur le tableau Les Ménines de Velasquez. Il nous avait proposé une analyse remarquable de ce tableau et fait passer une heure dans un monde bien différent de celui des mathématiques. J’avais été intriguée et impressionnée à l’époque par ce mathématicien- historien de l’art.
Plus tard, je l’ai retrouvé sur Toulouse, toujours dans une conférence d’histoire de l’art et j’ai découvert à cette occasion qu’il était complice d’Yves Lepestipon, professeur de littérature en classe préparatoire littéraire au lycée Fermat , et surtout artiste polyvalent. Au passage, Yves Lepestipon a réalisé un film sur le mathématicien Grothendieck. Finalement, les genres se brouillent et c’est tant mieux.

Denis est né à Paris en 1966. Il est originaire de Ménilmontant, Belleville. Il apprécie toujours ce quartier, « un des rares de Paris qui ait encore une âme ». Ses parents y vivent encore. Ce quartier cosmopolite et populaire a marqué son enfance. Il se souvient de l’épicerie, des artisans. C’était une ambiance de village au milieu de Paris.
Aimais-tu déjà les mathématiques dans ta petite enfance ?
J’ai sans doute eu une prédisposition pour les mathématiques parce que mon père est informaticien. Il m’a fait vivre une expérience marquante qui a déterminé ce que j’ai voulu faire par la suite. Il travaillait à l’époque à l’Office National de la Navigation, et il m’avait entrainé dans la salle des machines. J’avais six ans, c’était en 1972. Les ordinateurs d’alors étaient d’immenses coffrages, un peu comme ce que l’on peut voire dans 2001 Odyssée de l’Espace, le film de Stanley Kubrick. Il y avait donc ces immenses placards, des bandes magnétiques qui tournaient, dans un sens puis dans l’autre, il y avait une chaleur terrifiante, des cartons perforés avalés par la machine. Mon père m’avait expliqué que ces successions de pleins et vides dans les cartons symbolisaient des 0 et des 1. Le langage de l’informatique était un langage binaire. Il m’avait expliqué la logique, l’arithmétique binaire, etc. Tout cela avait vraiment frappé mon imagination. Je me disais « il y a des choses qui se passent, ces 0 et ces 1, ce bruit – tchou tchou tchou-. » C’était une insertion dans le monde magique des ordinateurs.
Paradoxalement, c’est aussi pour cela que j’ai fait très peu d’informatique. Cette expérience primitive était tellement forte. Maintenant quand je vois des ordinateurs, je ne retrouve pas le charme magique des cartons qui passent. Je vois que ça marche, mais j’ai perdu le contact presque charnel que j’avais pu avoir à l’époque avec ces machines.

Dans ma scolarité, j’étais bon en mathématiques, mais pas seulement. Je n’avais pas de prédisposition particulière pour une discipline. Vers 12-13 ans, je me suis mis à lire des articles de mathématiques dans l’Encyclopedia Universalis qu’avaient achetée mes parents. J’avais découvert cela tout seul, sans l’intermédiaire d’un professeur. J’ouvrais l’encyclopédie un peu au hasard. C’est quelque chose qu’on a un peu perdu actuellement. Avec internet, on ne trouve que ce que l’on cherche. On ne navigue jamais au hasard, on emprunte des routes tracées par les algorithmes. J’ai commencé à lire les articles sur les équations algébriques en particulier. J’avais aussi été fasciné par l’article sur la perspective. Sur les fonctions holomorphes et la logique, également. Je n’y comprenais pas grand- chose, mais le peu que je comprenais me laissait entrevoir la beauté. La beauté des formules, je les trouvais magnifiques, la beauté des dessins qui me semblaient extraordinaires. Je voulais absolument comprendre. C’était comme une langue étrangère. J’étais fasciné.
J’avais quand même réussi à comprendre les équations algébriques du troisième degré, et j’avais même refais les calculs pour voir par moi-même que cela marchait bien.
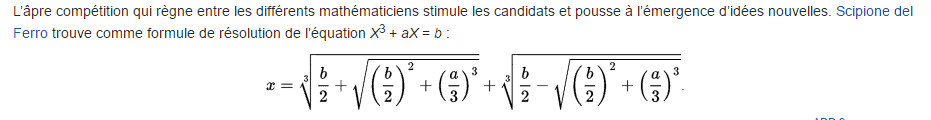
En fait à cet âge-là, on est un vrai buvard. Une fois un peu stimulé, on essaye de remonter à la source, de comprendre. Ce qui est remarquable en mathématiques, au contraire de la littérature où il faut avoir une expérience, une maturité pour comprendre les textes, pour les assimiler, c’est qu’il est possible de comprendre très jeune. Je trouve d’ailleurs dommage que l’on ne propose pas aux jeunes des activités plus intéressantes en mathématiques.
Je m’étais donc lancé avec ardeur dans les mathématiques, et je faisais des choses complètement indépendantes du programme enseigné.
L’école ne m’intéressait d’ailleurs qu’à moitié. J’avais des bonnes notes, pour moi c’était naturel et facile. Ce qui me plaisait, c’était mes recherches personnelles. J’aimais ça, je voyais la beauté des constructions logiques. J’étais animé de la passion du pèlerin qui part à la recherche de la vérité, je voulais comprendre ce qu’il y avait derrière les équations algébriques, avec une ferveur quasi mystique. Il fallait que j’accède à cette connaissance, au détriment du reste.
Je continuais quand même à travailler les autres matières. Je n’étais en effet pas tout à fait sûr de vouloir être mathématicien, il y avait également d’autres choses qui me fascinaient. Par exemple l’architecture. J’étais très sensible à la beauté de l’architecture. J’écoutais aussi beaucoup de musique, notamment Bach, qui est resté une de mes grandes passions. Avec l’école j’allais au musée du Louvre, les momies égyptiennes, les antiquités, tout cela me passionnait. J’en appréciais la dimension historique.
En terminale, vers 15-16 ans, je me suis mis en roue libre. J’avais suffisamment d’avance, je ne travaillais plus. Je passais autrement mon temps, je lisais, je vivais diverses expériences. Je ne savais pas ce que je voulais faire après le lycée, alors mes professeurs m’ont conseillé de faire des mathématiques pour commencer, d’aller en classe préparatoire scientifique. Je crois qu’ils ont eu raison et c’est aussi ce que je recommande aux élèves qui ne savent pas ce qu’ils veulent faire. Pour comprendre les mathématiques, il faut en faire entre 15 et 20 ans, de manière intensive, pour que les structures se mettent en place. Après, c’est très difficile à rattraper. Après 20 ans, on perd cette fraicheur, cette ouverture d’esprit.
Je suis donc allé en classe préparatoire au lycée Saint-Louis, (boulevard St-Michel à Paris). J’ai beaucoup aimé, j’ai bien apprécié les professeurs. J’étais enthousiasmé à l’idée de préparer un concours. Cela me donnait un objectif. Et puis, j’aimais bien résoudre des problèmes. Je m’étais remis à faire des mathématiques à plein temps. Un peu de physique aussi, j’aimais comprendre la structure, en particulier la théorie de la relativité, qui nécessite beaucoup de mathématiques, ainsi que la mécanique quantique. Je n’aimais pas trop la chimie par contre, ça me paraissait un peu de l’arrière cuisine, ce côté un peu empirique me désolait. Alors qu’en physique, on fait des raisonnements, il y a des choses à comprendre. Je ne travaillais pas non plus tant que cela à l’époque, j’avais le temps de suivre des cours de philosophie à la Sorbonne, en particulier ceux de Michel Serres. (Le lycée st Louis et la Sorbonne sont tout à côté). A l’époque on rentrait et on s’asseyait dans l’amphithéâtre, il n’y avait pas de contrôle.


En mathématiques j’aimais énormément la géométrie, et l’algèbre. L’algèbre en particulier permet d’obtenir très rapidement, à partir de quelques définitions, des résultats fascinants.
Je me posais des questions, par exemple je me demandais pourquoi les structures de groupes, de corps, d’anneaux, on les définissait comme cela et pas autrement. Il y avait la question de la nécessité qui me taraudait. Pourquoi on a besoin de cette axiomatique ? A l’époque c’était encore l’enseignement « bourbachique » (Nicolas Bourbaki est le pseudonyme d’un groupe de mathématiciens qui ont eu pour projet de réécrire complètement les mathématiques, de manière très formelle et axiomatique, et ont beaucoup influencé l’enseignement des mathématiques en France), où on nous enseignait une théorie complètement achevée. On partait des axiomes de Zermelo-Fraenkel, de la théorie des ensembles, et puis on fondait tout de but en blanc. Mais il n’y avait pas de justification. Mes professeurs expliquaient très bien, on avait l’impression d’une grande pureté, d’une sorte d’intemporalité. Mais ce qui me gênait, c’est qu’on évacuait toute la dimension historique. Qu’est-ce qu’il y avait derrière, pourquoi cela avait-il été élaboré, quels avaient été les errements, les erreurs ? Pourquoi ces théories-là ?
Mais enfin, et c’était une grande joie, je comprenais les équations algébriques ! Les questions que je m’étais posées à 12-13 ans avaient finalement obtenu une réponse définitive, avec la théorie de Galois. Je me souviens m’être dit, quand j’ai eu fini d’étudier la théorie de Galois, « ah voilà la raison profonde pour laquelle ces équations sont résolues et pas d’autres ». J’avais une explication. C’était une sorte d’achèvement. J’ai ressenti un grand soulagement, et une espèce de joie : tout s’expliquait enfin! L’énigme était résolue. Bien sûr, c’était d’autres qui avaient élaboré la théorie, mais au moment où je l’ai lu, où je l’ai comprise, je me la suis appropriée. C’est devenu quelque chose de naturel pour moi. C’est vraiment une chose qui est importante pour moi, et que j’essaye de transmettre dans mon enseignement, c’est qu’on peut s’approprier les théories mathématiques. Au moment où on les comprend, c’est vraiment à soi. Ce n’est pas quelque chose d’artificiel. Quand on redémontre un théorème, on a vraiment l’impression de comprendre profondément la chose.
J’ai intégré l’Ecole Normale Supérieure de la rue d’Ulm, en 1986. J’ai alors connu ce qu’on pourrait appeler une crise existentielle. J’avais une liberté absolue. Dans cette école, on avait 20 ans, on faisait ce qu’on voulait. Il n’y avait pas d’objectif, on était livrés à nous même. Il n’y avait pas non plus de relation privilégiée, quasi filiale, avec un enseignant, pas de figure prépondérante. J’avais trouvé cela désorientant. Dans ma promotion il y avait des camarades très doués, Laurent Lafforgue par exemple, et dans la promotion suivante Wendelin Werner. (Ces deux mathématiciens ont obtenu la médaille Fields ) . J’ai rencontré des gens brillants intellectuellement, c’étaient des années riches. Mais est-ce que j’avais vraiment envie de vivre comme les mathématiciens que je voyais autour de moi ? Là c’est posé la question de l’existence. J’ai découvert en particulier qu’il fallait faire carrière, avoir des postes…Il y avait tout un coté administratif qui m’a refroidi. Est-ce que j’ai envie de ressembler à ces gens-là ?
Tu avais l’impression que pour réussir à l’Université et faire carrière il fallait faire preuve de compromission ?
J’avais l’impression qu’on ne faisait pas des mathématiques pour les mathématiques, et que pour pouvoir en vivre, il fallait choisir un domaine en particulier. Quand on devient très spécialisé dans un domaine en mathématiques, ça devient vraiment compliqué de communiquer avec les autres. Il y a très peu gens qui comprennent ce qu’on fait. Le côté positif de faire des mathématiques à plein temps, dans un domaine très pointu, c’est l’enthousiasme absolu de se sentir à la pointe de la recherche. Mais c’est enfermant aussi. Je trouvais ça dommage de m’enfermer là-dedans. J’avais envie de faire plein d’autres choses. En tout cas ces années m’ont ouvert les yeux sur ce qu’était une carrière de mathématicien, et je n’en ai pas eu envie.
Parallèlement à ce que je faisais en mathématiques à l’ENS, je suivais des cours d’histoire de l’art. Bon évidemment c’est complètement orthogonal… En particulier, par rapport au milieu mathématique où les femmes étaient sous-représentées, il y avait beaucoup de filles dans le milieu de l’histoire de l’art. Le summum a été dans le cours d’art paléochrétien où on était deux garçons pour quatre-vingt-quatre filles. C’était vraiment l’inverse du milieu mathématique! C’était plutôt bien. C’était aussi beaucoup plus incarné, il y avait les tableaux que l’on pouvait voir, et également une dimension historique. On essayait de comprendre ce que des gens ayant vécu il y a 500 ans, 600 ans, avaient bien pu vouloir dire dans leur peinture. C’était des objets réels, ayant un sens. Et on regardait toute la civilisation autour. C’était plus ouvert sur la société.
J’ai passé en parallèle l’agrégation de mathématiques, pour arrêter de faire des mathématiques justement, finir mon cursus. Cela peut paraître paradoxal…Puis j’ai pris deux ans de congé sans traitement pour rattraper mon cursus en histoire de l’art et enchainer sur des études plus approfondies. J’ai fait ensuite des recherches sur les primitifs flamands. C’était un nouveau défi, un peu comparable à celui que je m’étais donné à 12-13 ans, en voulant comprendre les équations algébriques. Je voulais comprendre ce qui se passait dans la peinture flamande. Une question que je m’étais posée à propos des peintre flamands, c’est qu’ils avaient révolutionné la peinture avec leur techniques picturales, mais ils n’avaient absolument rien écrit. Pas de théorie. Alors qu’en Italie, quand s’est produite la grande révolution de la perspective, il y a eu énormément de traités théoriques. Pourquoi y avait-il une séparation entre la théorie et la pratique chez les flamands ? Ce que j’ai essayé de prouver, c’est que les flamands avaient incorporé la théorie à la pratique. Leurs peintures sont des objets théoriques en tant que tels.

Après la Sorbonne je suis entré à l’EHESS (Ecole des Hautes Etudes en Sciences Sociales) et c’était très bien, j’ai rencontré des gens d’une grande ouverture d’esprit, d’horizons variés, parfois étrangers, des gens avec qui je pouvais parler, partager mes passions.
Puis est venu le temps de gagner ma vie.
Pendant mon service militaire, j’avais enseigné à une classe de maths spé, au Prytanée Militaire. C’était en tant que mathématicien que j’avais le plus de chance d’éviter d’être dans des unités en dehors du territoire ou de devoir passer dix mois dans une caserne. C’était des conditions spéciales, mais j’avais découvert l’enseignement. J’avais trouvé ça plutôt agréable d’enseigner, et d’enseigner les mathématiques en particulier. Il y a des choses très claires à faire comprendre. En fait le plus difficile dans l’enseignement des mathématiques, c’est de comprendre pourquoi c’est difficile pour les autres. Pourquoi, les élèves bloquent à ce moment-là, alors que ça me paraît évident ? J’avais déjà cette préoccupation à l’époque de présenter les choses de façon à ce que les élèves puissent s’approprier les objets. Que ça leur paraisse naturel. Je cherchais des présentations. Je devais sortir de moi-même et imaginer ce que pouvait ressentir un autre.
Après mon service militaire, je suis revenu à Paris, et au moment de gagner ma vie, le plus simple et le plus pratique pour moi fût d’enseigner les mathématiques en classe préparatoire. En 1993 j’ai été nommé à Bordeaux, et j’y suis resté depuis. Je m’y suis beaucoup plu.
Comment occupes-tu ton temps entre les mathématiques et l’histoire de l’art ?
L’essentiel de mon activité c’est l’enseignement. C’est très enrichissant. Chaque année je trouve les élèves de plus en plus jeunes…, sans me rendre compte que c’est moi qui suis de plus en plus vieux…
Je ne fais pas de recherche en mathématiques. A l’Ecole Normale, j’avais commencé un DEA sur les groupes de Lie mais j’ai tout arrêté après l’agrégation.
Je continue à faire des recherches en histoire de l’art, toujours autour de la perspective, et des anamorphoses en particulier. J’écris des articles, je fais chaque année des conférences dans différents cadres, sur la perspective, sur la peinture généraliste, j’interviens en particulier à l’Université Populaire à Bordeaux.
Je me suis beaucoup intéressé à l’histoire de la perspective. J’ai écrit un livre sur le sujet, intitulé Douce perspective, (Editions Ellipses).
C’est l’histoire de la rencontre entre l’art et la science. L’histoire d’un objet, complètement pictural au XVème siècle, qui a été récupéré deux siècles plus tard par les géomètres. Ce moment de transition où les mathématiciens ont inventé la géométrie projective, qui est pour moi une des plus belles créations de l’esprit humain.
Ce que je fais en histoire de l’art a un lien avec les mathématiques. La perspective est vraiment à la croisée des deux mondes. Entre art et géométrie. C’est un domaine assez bien exploré, mais assez peu d’un point de vue mathématique. Ce modèle s’est d’abord incarné dans la peinture puis plus tard dans la géométrie. Il a fallu un long temps de latence aux mathématiciens pour qu’ils se rendent compte de toute la profondeur conceptuelle derrière la perspective. Desargues en particulier, qui pour moi est un des grands mathématiciens que je vénère par-dessus tout, s’est posé la question de la mathématisation, des points à l’infini, des transformations, des anamorphoses,…
Desargues est un des grands révolutionnaires de la pensée mathématique. La perspective , c’est vraiment le moment où la Renaissance a lieu. Les peintres se sont rendu compte qu’ils avaient là quelque chose que les anciens n’avaient pas, quelque chose de vraiment nouveau.
Au moyen âge, les gens s’imaginaient qu’ils étaient dans la perpétuation de ce qu’avaient fait les grecs. Et quand Brunelleschi invente la perspective en 1415, il prend conscience de cette rupture de tradition. On est passé à autre chose. De même Galilée révolutionne la physique. Il faut s’approprier le langage mathématique pour décrire le monde physique. On sort du paradigme de l’Antiquité où les mathématiques sont déconnectées de la réalité et sont peu appliqués. Pendant la Renaissance, il y a concordance entre la science, l’art et la pensée. Ils essayent de comprendre le monde, de l’interpréter, d’en construire toutes les structures. Le langage mathématique s’impose à ce moment-là.
Y a-t-il des civilisations qui ne connaissent pas le langage mathématique ?
Toutes les civilisations ont fait des mathématiques. Les babyloniens connaissaient l’équation du second degré. Mais il n’y a pas cette volonté d’axiomatiser, de fonder les mathématiques sur des axiomes. Cette démarche est spécifique à l’Occident. On veut fonder les choses en raison. Dans les autres civilisations l’approche est plus empirique, ils ne voient pas les mathématiques comme une langue. De mon point de vue c’est un langage propre. Le langage dans lequel le monde est écrit. Il est naturel mais n’est pas parlé spontanément. Il est naturel mais pas natif. Il faut se l’approprier. Il faut d’abord faire la grammaire avant de parler.
Quelle est la place des mathématiques dans ta vie ?
C’est très structurant. Les mathématiques c’est une espèce d’école de vérité. C’est ça qui est fondamental. On cherche à comprendre pourquoi c’est comme ça et pas autrement. On se pose très vite les questions de la nécessité et du hasard. Quand je me promène dans la rue, dans ma vie quotidienne, j’essaye toujours de comprendre ce qu’il y a derrière ce que je vois. Le modèle mathématique c’est la recherche de la plus grande universalité. On voit un phénomène particulier, on cherche ce qu’il y a derrière, ce qu’il y a de plus grand, de plus général. J’essaye de rattacher ce que je vois à d’autres objets. Je recherche la structure commune. Pour moi, le mathématicien c’est celui qui va chercher le bon point de vue pour trouver la plus grande universalité. C’est un peu comme si on était plongé dans un tableau et qu’on en voit que des détails. Le mathématicien c’est celui qui va essayer de prendre du recul pour voir le tableau dans son ensemble.
Faire des mathématique, c’est chercher le sens.
Est-ce que tu appliques cela aussi aux relations humaines ?
Oui, tout à fait. Je pense qu’on est préfiguré pour avoir des affinités avec certaines personnes. Pourquoi on est attiré par ces personnes ? Quelle est la structure ? C’est une série d’accidents, mais il y a un sens. C’est un peu une démarche psychologique, si tu prends le recul suffisant, il y a une cohérence d’ensemble qui se dessine.
Ton milieu familial a-t-il compté ? J’ai l’impression que tu t’es un peu fait tout seul.
Mon père me montrait des mathématiques, mais jusqu’à ce que j’intègre l’Ecole Normale, il n’y avait personne avec qui je pouvais vraiment communiquer en mathématiques. J’avais toujours cette idée, que profondément si je voulais comprendre, cela ne pouvait qu’être une démarche personnelle. J’étais assez isolé quand j’étais enfant. Ce n’est que tardivement que j’ai trouvé des gens qui me ressemblent, avec qui je peux communiquer.
Quel est ton mathématicien préféré ?
J’accorde une grande importance de la dimension historique, qui n’est pas assez développée dans l’enseignement. Quand on enseigne une notion, il faudrait se rapporter à l’époque où les gens se posaient ces questions. Les professeurs évacuent trop souvent la dimension historique ; ils se contentent d’avoir une belle théorie. L’histoire apprend à comprendre la profondeur, les errements, le temps mis à élaborer une théorie.
J’aime les mathématiciens un peu décalés. Desargues était un peu dilettante, mais à l’époque, ils faisaient tous – Descartes, Desargues, Pascal,….- autre chose. Ils se connaissaient tous d’ailleurs. Ils avaient des échanges épistolaires fabuleux.
Desargues invente la géométrie projective, l’anamorphose. Les coniques sont des anamorphoses de cercle, des cercles en perspective. Les grecs n’avaient pas vu du tout les choses comme ça. Il est arrivé à trouver le bon point de vue sur les coniques. Il a des titres assez poétiques : Le brouillon projet d’une atteinte aux évènements de la rencontre du cône avec un plan. Il avait un vocabulaire imagé.

Grothendieck aussi est un grand inventeur de mots, un poète.
Nommer les choses en mathématiques ce n’est pas innocent. On essaye de trouver un mot parlant, imagé, compréhensible, qui donne une image correcte de la notion. Les mathématiciens vont prendre un mot du langage usuel et vont l’utiliser pour donner une image de l’objet qu’ils manipulent. On dit que les mathématiques sont très abstraites. C’est une grande méprise. Pour les mathématiciens, elles sont très concrètes. Les compacts, les connexes, groupes, anneaux, corps… Les mathématiques ne sont pas déconnectées du réel, elles sont très incarnées. On touche, on manipule. Il y a un côté charnel. Il y a un malentendu sur ce que sont les mathématiques. Ceux à qui on les enseignene se rendent pas compte à quel point ce sont des choses concrètes.
Mais pourquoi ? Qu’est-ce qu’il manque à l’enseignement ? Comment fais-tu?
J’enseigne dans une classe où il y a malheureusement, de ce point de vue, il y a l’objectif du concours. Mais j’essaye de donner une perspective historique. En expliquant pourquoi une théorie n’a pas du tout été évidente dès le départ. Je m’efforce de montrer comment ça se construit petit à petit. Il est très important de manipuler. On part d’un résultat, on expérimente, et on trouve après le théorème. Il ne faut pas forcément chercher la généralité en premier. Les mathématiques, c’est comme un tableau de Rembrandt . Au départ on voit l’épaisseur de la croûte, le flou, le net, le clair-obscur. Et quand on recule, on comprend, on découvre le tableau.
Quelle est ton équation ou ta formule préférée?
Cette formule, trouvée par Euler, me fascine. Je dis aux élèves que quand il y a une belle formule en mathématiques, c’est soit Euler soit Ramanujan. On ne sait pas d’où ça vient.
Dans cette formule, il y a le sinus, il y a une factorisation, et en plus elle permet aussi de prouver que
Elle n’est pas innocente, elle a des conséquences énormes. Et pourtant quand on la regarde elle est complètement naturelle. C’est comme si c’était un polynôme. On a cherché les racines, les points où il s’annule, et on l’a mis sous forme factorisée.
Pour qu’une formule soit belle, il faut qu’elle ait ce côté évident, simple. Comme une statue grecque. Il faut qu’il y ait la grâce. C’est indéfinissable. Mais c’est important aussi qu’il y ait des implications, que ça fasse réfléchir. Que ça puisse s’incarner, s’accomplir.

C’est quoi ta définition des mathématiques ?
C’est une école qui apprend à chercher le bon point de vue sur ce que l’on a sous les yeux. C’est lié à la perspective aussi. C’est également la recherche d’un point de vue commun. L’endroit où les choses communiquent, plus ou moins secrètement.
Est-ce important de faire des mathématiques à l’école ?
Le grand drame de l’enseignement c’est qu’on y présente les mathématiques comme quelque chose d’achevé. Il faudrait prendre le temps pour que l’objet devienne personnel et que chacun puisse lui donner un sens. On a tous des visons différentes, intimes, des objets. On parle de la même chose, mais on n’en a pas du tout la même image. L’idéal serait de faire en sorte que chacun ait sa représentation personnelle. C’est très difficile.
Qu’est que ça apporte les mathématiques dans le domaine du développement personnel ?
C’est la recherche de la vérité. Plus précisément, la recherche des procédures qui mènent à la vérité. Qu’est-ce que je sais, qu’est-ce que je ne sais pas ? C’est une question fondamentale en mathématiques et dans la vie en général. On y apprend à raisonner. C’est également l’acceptation du fait que l’on doive avoir des procédures de justification acceptables par les autres. Cela permet d’entrer dans la vérité partagée.
Tout le monde n’a pas la même vérité ?
En effet, mais on peut essayer de partager les méthodes de validation.
Stendhal explique cela très bien. Quand on a un point de désaccord sur un objet, une vision d’une chose, on met de côté toutes les propriétés inintéressantes. On oublie un certain nombre de choses, jusqu’à ce qu’on arrive à se mettre d’accord. C’est la quête des lois communes que chacun peut admettre.
Envisages-tu continuer à faire des mathématiques même sans nécessité professionnelle?
Oui.
Hilbert a fait écrire sur sa tombe « nous devons savoir, nous saurons ».
C’est une école de curiosité. Il y a des choses à comprendre et chacun peut y avoir accès.