Introduction

Dans ma pratique de psychopédagogue spécialisée dans les blocages en mathématiques, j’ai noté que les principales difficultés des élèves viennent d’une incompréhension sur le concept de « comprendre son cours ». Ils expriment souvent leurs difficultés par « j’ai compris mon cours, mais je ne sais pas faire les exercices ». Ce à quoi je rétorque «  si tu ne sais pas faire les exercices, c’est que tu n’as pas compris ton cours ».

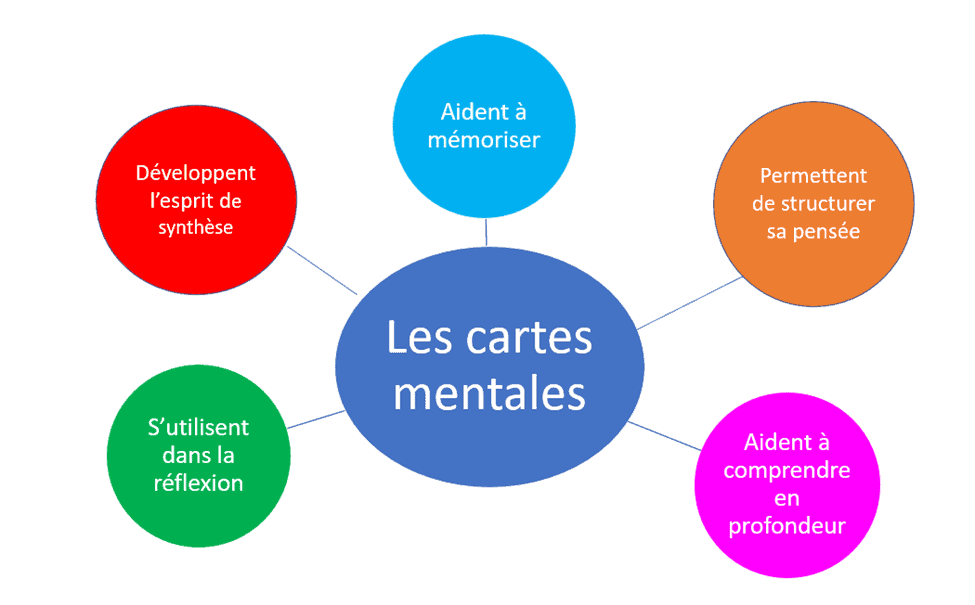
Les cartes mentales sont un très bon outil pour comprendre, mémoriser et réfléchir. Je vais exposer dans cet article comment j’accompagne les élèves à les construire et les utiliser.

Toutes les cartes mentales que je dessine et utilise en séance sont en format A4 paysage. Pourquoi ? parce que le champ de vision humain étant plus large que haut, écrire dans le format paysage permet d’englober toutes les informations et de faire des liens entre différentes parties.

Vous pouvez retrouver les cartes mentales des cours de seconde, première et terminale, ainsi que les cartes essentielles en prépa dans la boutique du site

Les différents types de cartes mentales

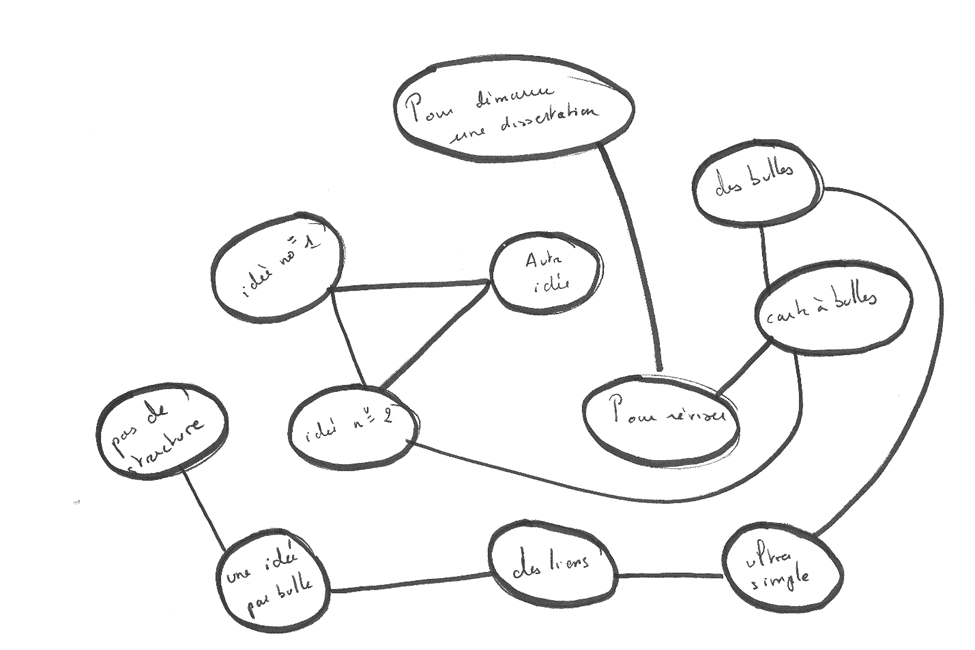
Les cartes à bulles

La carte à bulle est la première étape pour créer une carte mentale plus structurée. C’est aussi la première étape dans le processus de mémorisation.

Il s’agit d’écrire tous les mots/concepts qui viennent à l’idée sur un thème, un mot/concept = une bulle, en vrac sur une feuille, librement, sans structure.

Ensuite, on relie entre eux les concepts qui ont un lien, et une structure commence à apparaître.

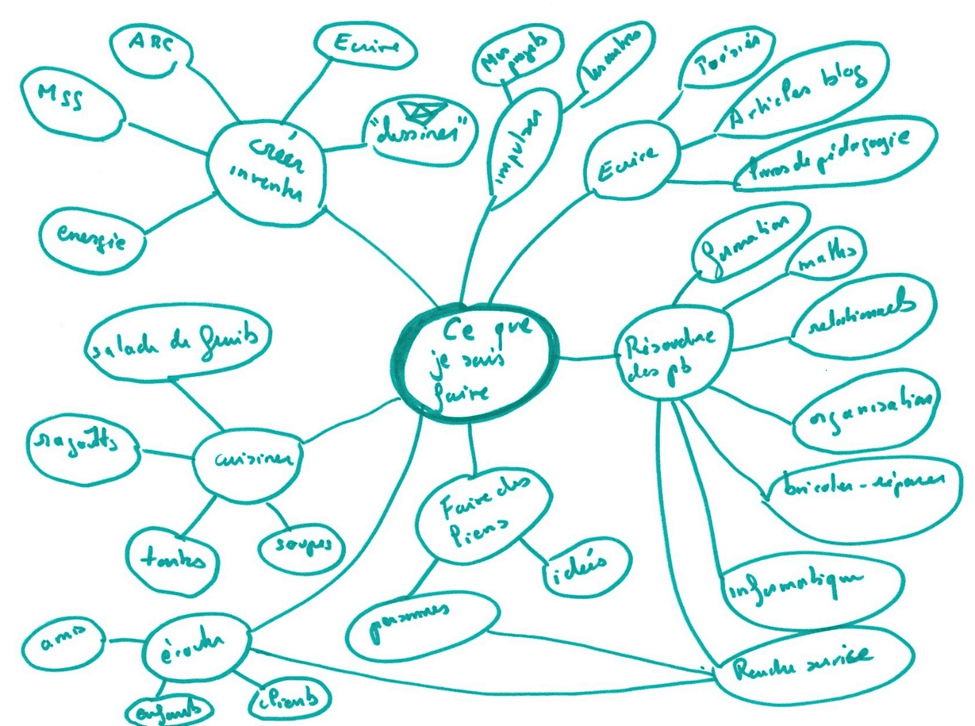
Les cartes centrées

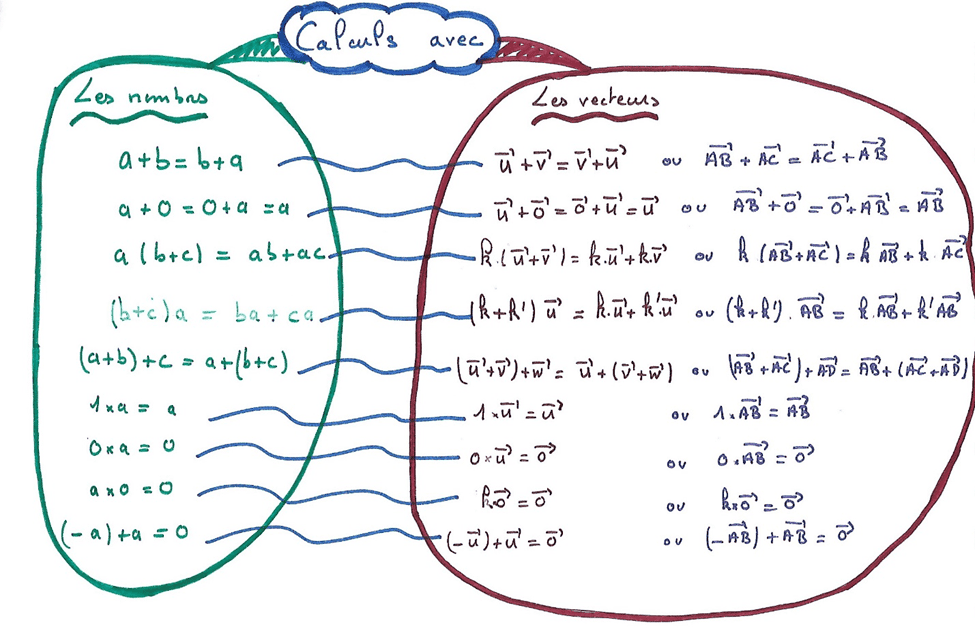
Une carte centrée, comme son nom l’indique, est structurée autour d’un centre, le thème principal. De ce cœur partent des branches, chaque branche concernant un sous-thème. Chaque sous-thème peut également se diviser en sous-sous thème et ainsi de suite. Pour ma part, en mathématiques, je me contente d’un seul niveau. Une carte se lit dans le sens des aiguilles d’une montre, en commençant en haut à droite. Chaque sous-thème est dans une même couleur, et il est préférable d’alterner les couleurs chaudes et froides, pour bien les distinguer visuellement.

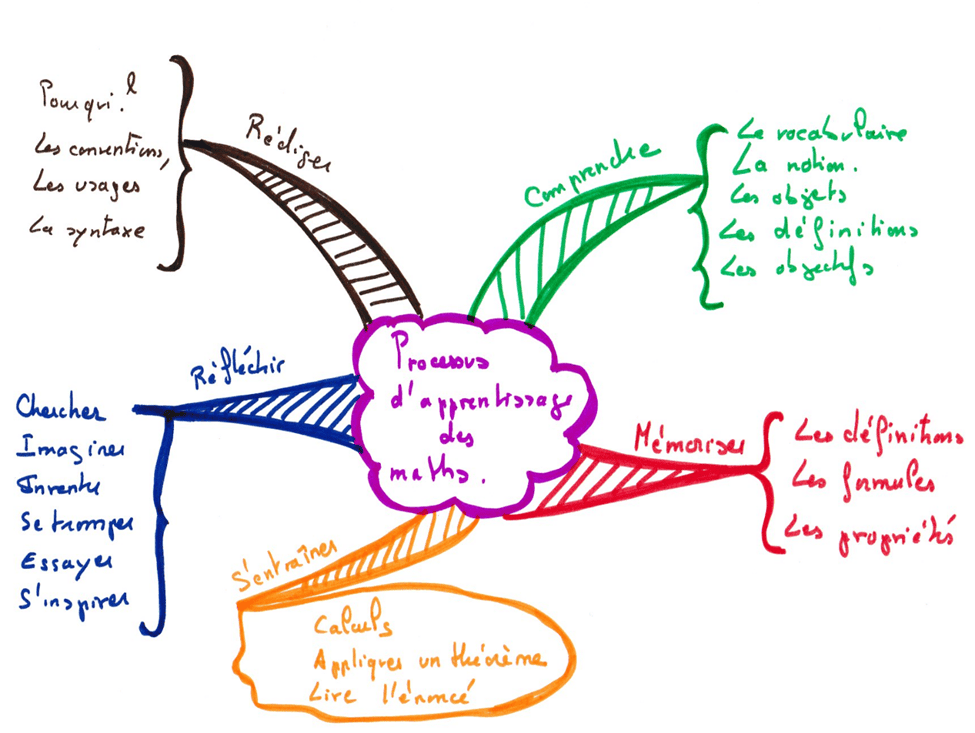
Il peut y avoir une suite logique, mais pas obligatoirement, comme dans l’exemple ci-dessus (les différentes actions ne sont pas forcément faites dans cet ordre).

On peut également matérialiser un lien spécifique entre deux sous thèmes, ou faire une bulle à part, comme une remarque ou un rappel.

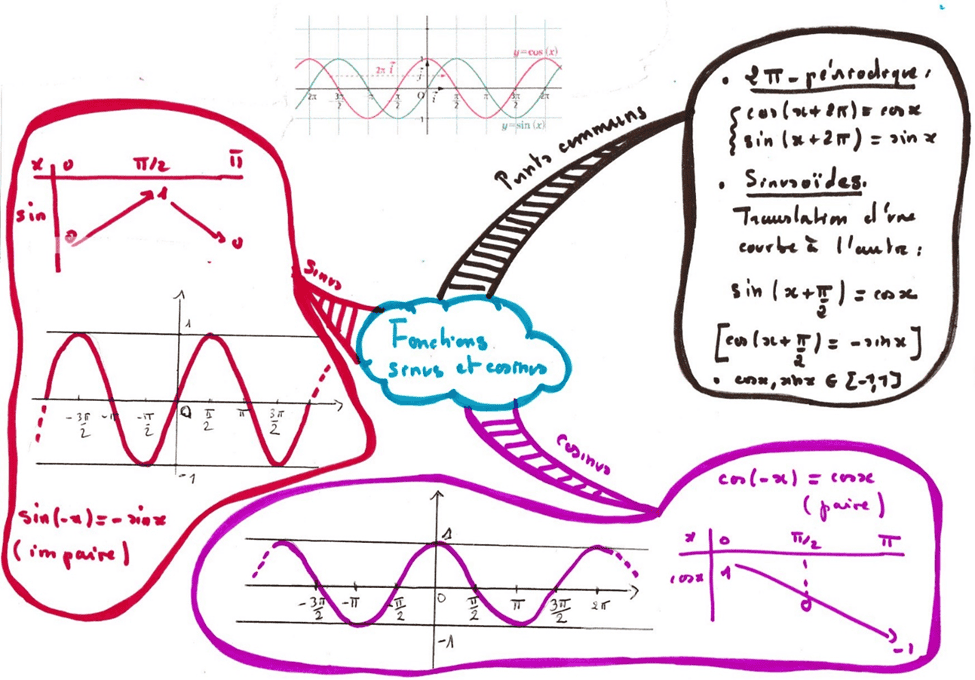
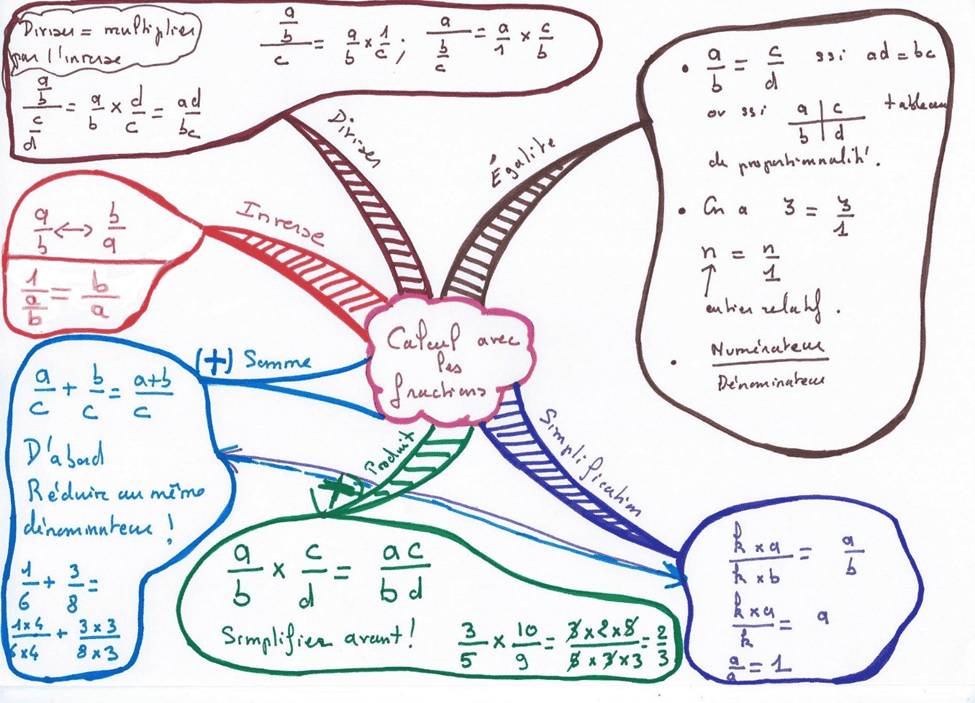
Une carte mentale est personnelle, et n’a pas à être rédigée comme un cours. Néanmoins, il ne faut pas oublier la rigueur mathématique. Pour faire comprendre aux élèves les attendus, je leur dis que c’est comme un pense-bête pour faire un cours, pour qu’ils n’oublient pas de parler de toutes les notions. « Il s’agit de faire le prof ! » m’a dit un jour un élève, et c’est tout à fait le cas. Par exemple, dans une carte mentale, il n’y a pas à mettre les démonstrations. Sauf, évidemment si on fait une carte mentale spécifiquement sur une démonstration.

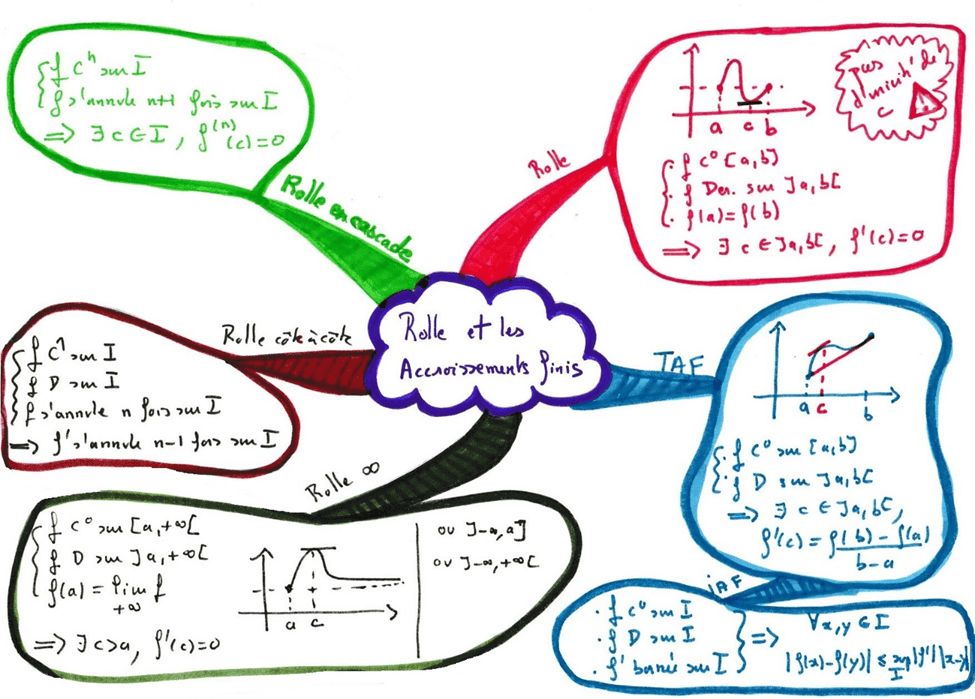
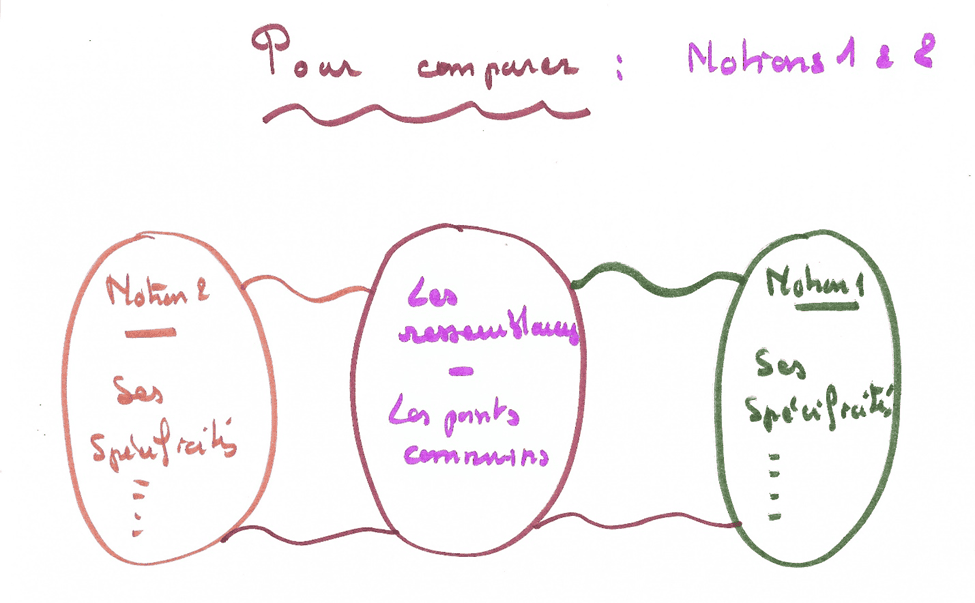
Les triples bulles, pour comparer et pour discriminer

Cette carte est utile quand on confond deux notions, ou quand on veut différencier deux concepts qui ont néanmoins des points communs. Elle est composée de trois grandes « bulles » côte à côte. Dans la bulle du milieu, on met les points communs et dans les bulles de droite et gauche les points spécifiques. Chaque bulle a une couleur différente.

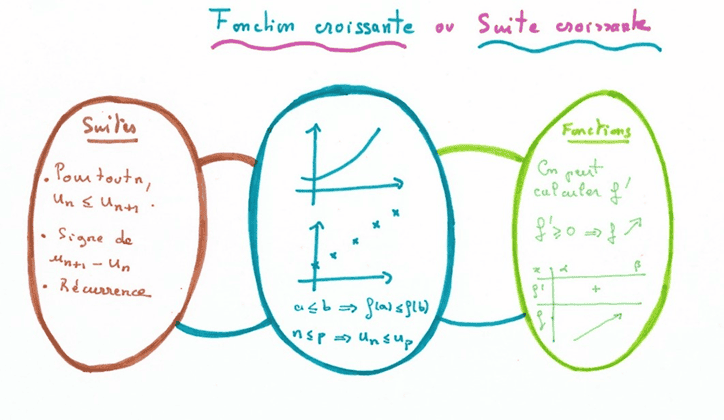
Construction d’une carte mentale

Je propose ici trois méthodes pour construire une carte mentale. Il est important de préciser à chaque fois que ce ne sont que des propositions, et que l’élève est libre de faire comme il veut ! La liberté et la créativité sont deux points essentiels pour que ce soit efficace. Mais comme dans tout, avant de faire ce que l’on veut, il faut avoir appris à faire, c’est pourquoi j’accompagne les élèves dans la construction de leurs cartes mentales avec ces trois méthodes.

Avec les 5 questions pour comprendre

Les cinq questions pour comprendre sont inspirées du travail de Guy Sonnois en gestion mentale.

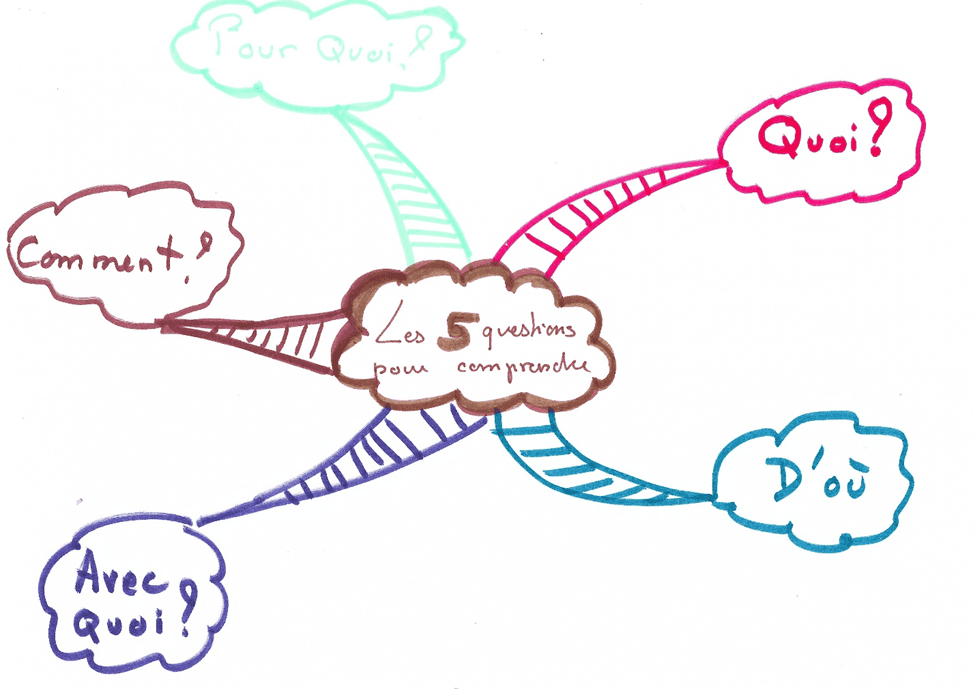
Je commence toujours par la question Quoi ?

Quoi ? : Cette question concerne la définition des objets mathématiques concernées. A la fois « comment je vois l’objet, comment je me l’imagine, quelle histoire je me raconte à son propos, comment je pourrais l’expliquer à quelqu’un qui n’y connait rien (un camarade qi aurait été absent par exemple) », et aussi, en parallèle, quelle est la définition qu’on m’a donné en cours.  Comme dit David Bessis :

Quand on étudie les espaces vectoriels, on étudie aussi les notions de dimension, d’application linéaire, de rang, de noyau…
Généralement on représente les espaces vectoriels par des lettres et les applications linéaires par des flèches reliant ces lettres. Mais quand je choisissais de voir les espaces vectoriels comme des récipients plus ou moins grands (selon leur dimension) et les applications linéaires comme des tuyaux plus ou moins gros (selon leur rang), alors tous les exercices qui portaient sur ces notions devenaient évidents. (Bessis D, Mathematica, 2022, Seuil, page 123)

Cette vision personnelle l’a clairement aidé à manipuler cette notion. Néanmoins, il faut aussi connaître la définition mathématique.

C’est le moment de prendre conscience de la double utilisation d’une définition (comment je démontre que c’est bien une application linéaire par exemple, et à quoi ça me sert de le savoir).

Il y a aussi une question concernant l’aspect de cet objet dans un exercice (comment je sais qu’il s’agit d’une suite, d’une fonction, etc.)

Il ne s’agit pas de répondre à toutes les questions de manière exhaustive, cela dépend du thème.

On cherche les réponses à ces questions dans les activités préliminaires, et dans les définitions du cours et les exemples.

D’où ? : On peut aborder cette question d’un point de vue historique, » à quelle époque et pour répondre à quelles problématiques est apparue telle ou telle notion ? », mais cela est rarement exposé en cours. Je propose également d’interpréter cette question par « de quelles notions mathématiques ai-je besoin pour travailler ce nouveau chapitre ?, Quels sont les chapitres utiles dans ceux qui ont été faits précédemment ? ». Cela permet de faire des liens entre les différentes notions mathématiques, et de réviser si besoin.

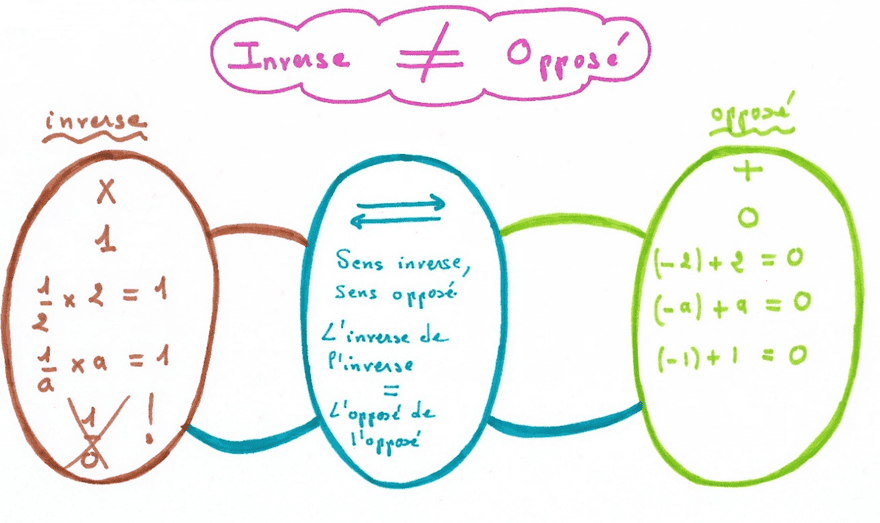
Avec quoi ? : est la question concernant les associations d’idées. La capacité à faire des associations d’idées est fondamentale pour la réflexion, autrement dit pour faire un exercice de mathématiques. On peut déjà partir du vocabulaire, les mots mathématiques étant des mots du langage français, ils évoquent forcément quelque chose dans l’esprit de l’élève, qui peut être une aide ou au contraire apporter une confusion (par exemple « inverse » et « opposé », deux notions fréquemment confondues par les élèves). Cela permet de se rendre compte qu’on est en train de faire une confusion (dans ce cas il sera judicieux de faire une carte « triples bulles »), ou bien se rendre compte « que c’est pareil », ce qui facilite la mémorisation.

La question Comment ? concerne les théorèmes et propriétés du cours. Cela permet de se rendre compte de ce qu’on peut faire avec ces objets, comment on peut les manipuler. Ce sont les outils pour faire les exercices.

La question Pour quoi ? (Pour quoi faire ?) concerne les questions que l’on pose en exercices, les enjeux. Comment est construit un problème sur le thème, à quelles questions me permet de répondre tel théorème, quand est-ce que je dois y penser. Cela permet d’anticiper les questions que l’on va rencontrer en exercices, et de faire le lien entre les théorèmes et leur utilisation. Car c’est bien beau de connaître ses identités remarquables, si on ne sait pas que cela sert à factoriser, cela ne sert à rien.

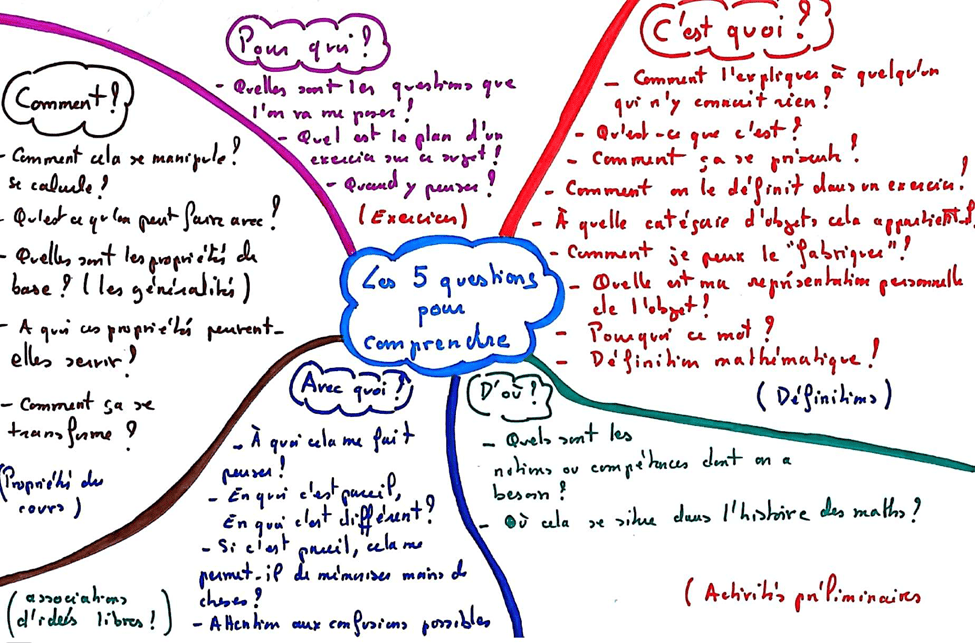
Voici des exemples de cartes construites avec cette méthode :

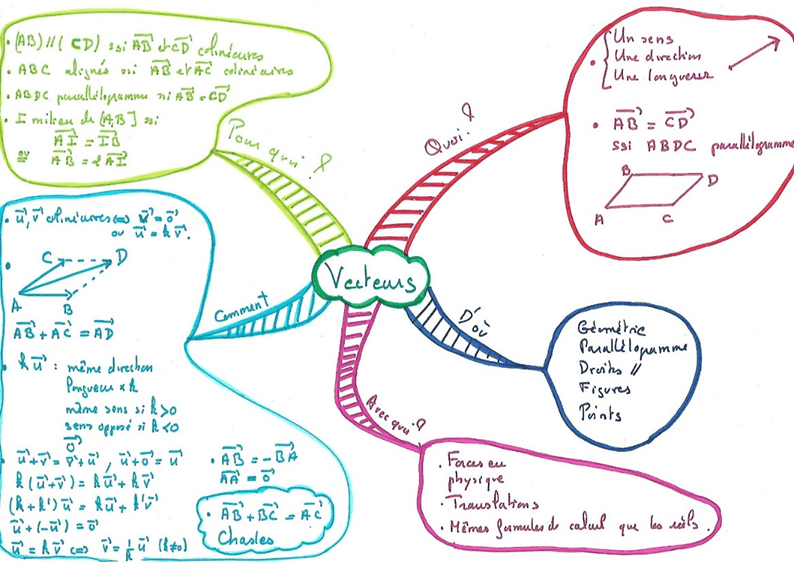
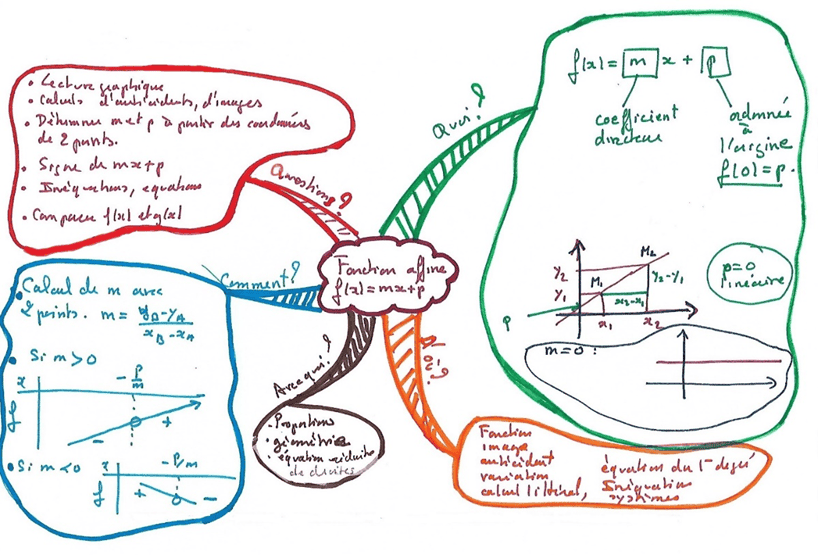
Par utilisation, techniques, questions posées en exercices

Cette méthode est bien adaptée pour retenir une technique, quasi algorithmique (résoudre une équation du premier degré par exemple), ou quand, face à un sujet, il y a un ordre de questions à se poser (pour étudier une limite ou la convergence d’une série par exemple). On peut aussi repérer qu’en exercices on pose souvent certaines questions et faire une carte suivant ce plan, ou encore quand il y a différentes manières de résoudre le même problème (montrer qu’une matrice est inversible par exemple).

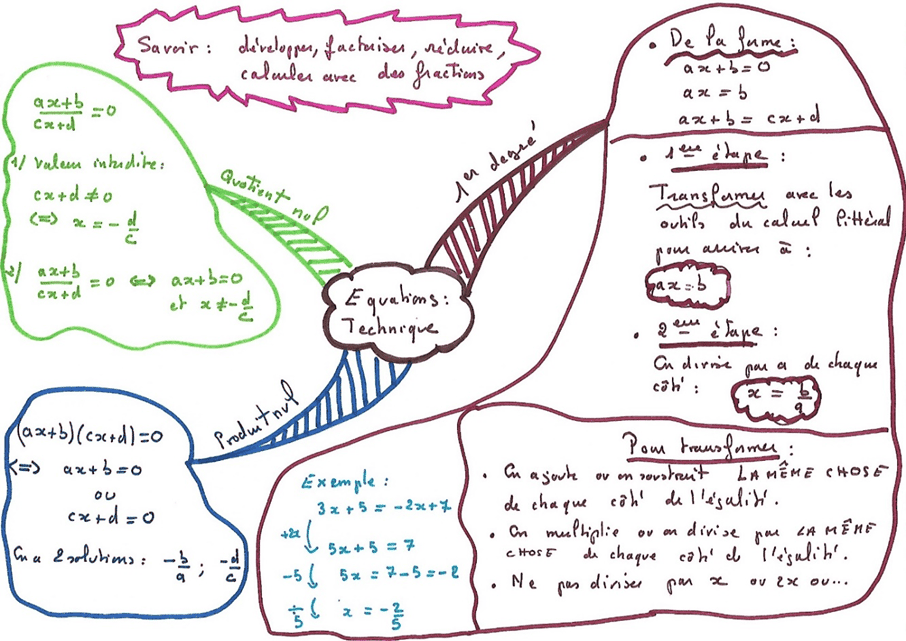
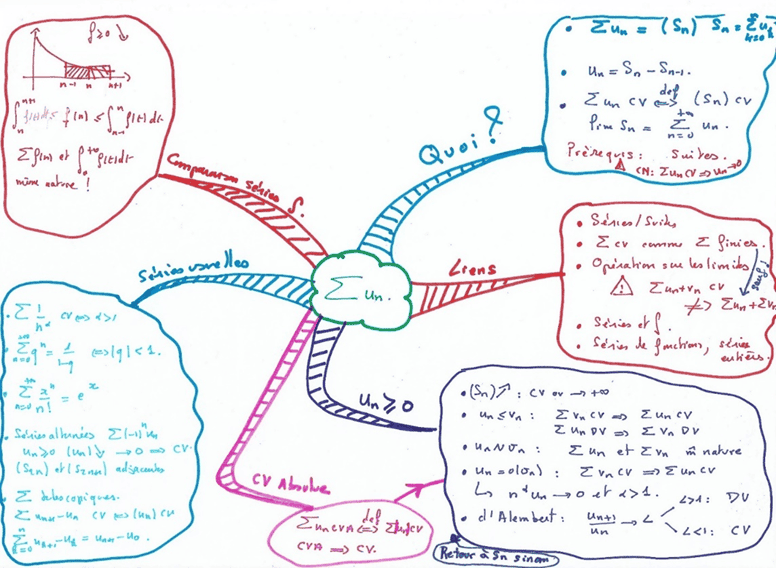
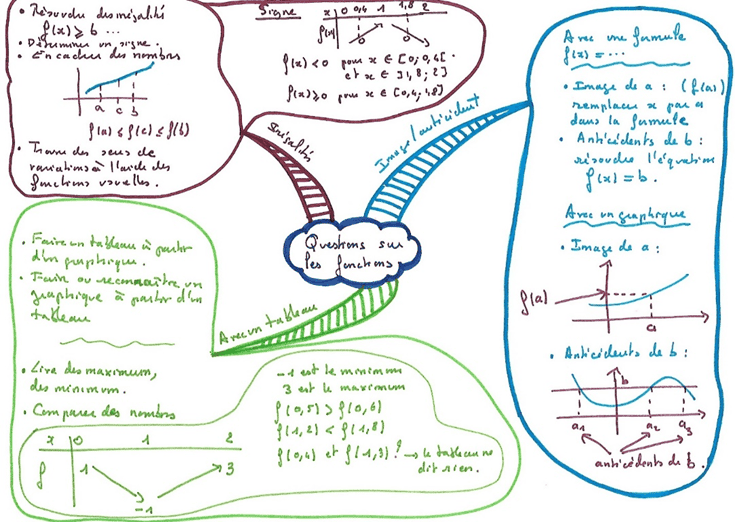
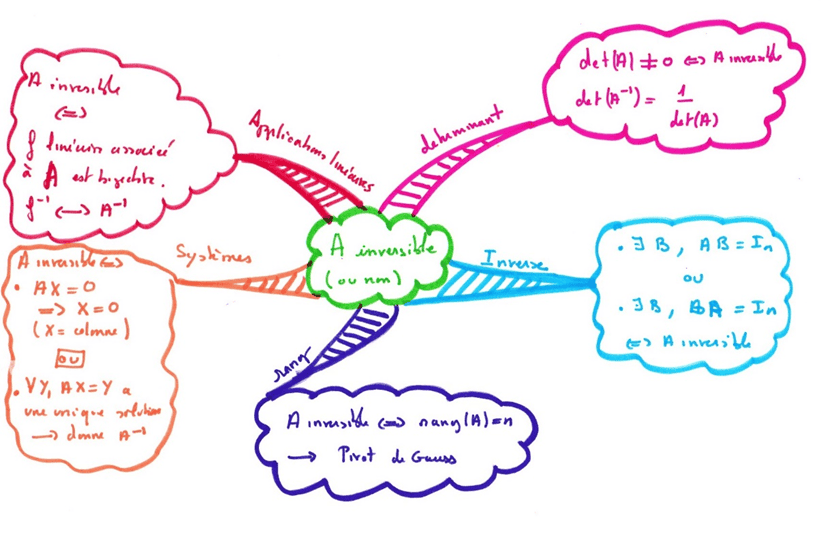
Avec le plan du cours

Il s’agit simplement de suivre le plan du cours. C’est souvent un bon début pour construire une carte mentale.

Comment utiliser ses cartes mentales ?

Une fois les cartes mentales faites, il s’agit bien de les utiliser ! Les utiliser permet également de se rendre compte si elles sont bien faites ou pas, c’est-à-dire si elles servent à « mémoriser, comprendre et réfléchir ».

Pour comprendre

Faire la carte mentale sur un thème, surtout si on se pose les cinq questions pour comprendre, permet justement de comprendre en profondeur la notion. On pourra noter que s’il est indispensable de se poser ces cinq questions, il n’est pas nécessaire de noter les réponses aux cinq questions sur une carte.

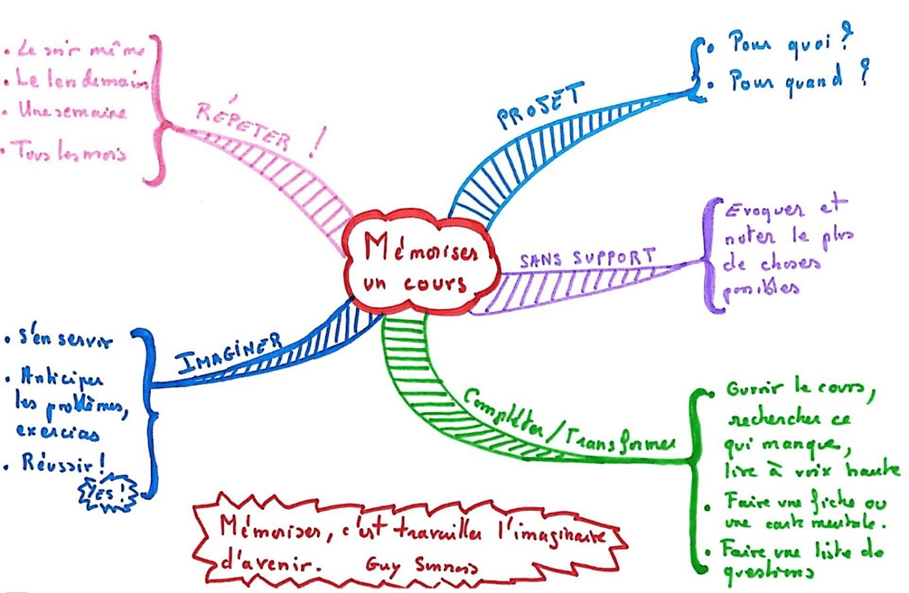
Pour mémoriser et réviser

Une fois la carte mentale faite, il reste à l’apprendre. Les couleurs et la disposition dans l’espace vont aider à la mémorisation. On peut également lire la carte à voix haute, et la raconter (dire des détails qui ne sont pas notés dans la carte). Idéalement, se mettre en situation de faire un cours (seul ou à un ou plusieurs camarades), en utilisant la carte comme pense-bête.

En mathématiques tout particulièrement, on ne peut pas se permettre d’oublier des notions, car tout sert à tout. Il faut donc garder ses connaissances actives. Chaque week-end, on peut se donner pour objectif de réviser deux ou trois notions vues précédemment. Pour cela on commence par recréer la carte mentale sur un brouillon, puis on compare avec l’original, et on complète si besoin.

Pour réfléchir

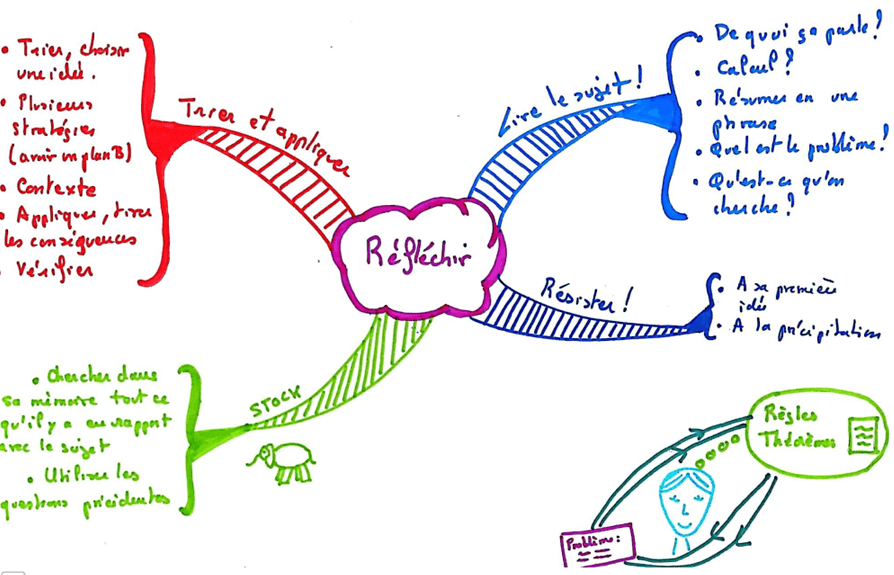
Réfléchir, c’est justement faire des allers-retours entre le problème posé et ses connaissances. Les idées ne viennent pas de nulle part, la solution n’arrive pas instantanément à l’esprit. Il faut justement aller la chercher. Mais où ?

Dans sa carte mentale justement ! Je préconise donc de faire les exercices avec la ou les cartes mentales sous les yeux, et de bien repérer quelle partie de la carte sert à quel genre de questions. Et aussi de matérialiser ces allers-retours par les mouvements des yeux, par l’énoncé à voix haute des propriétés utilisées. Cela permet en outre de renforcer la mémorisation.

Conclusion

Sans en faire une panacée indispensable, j’ai constaté dans ma pratique en libéral depuis 10 ans, que faire des cartes mentales est d’une grande aide pour la plupart des élèves. Bien sûr au départ, il faut accompagner les élèves dans la réalisation des cartes. Puis rapidement, ils s’emparent de cet outil, et s’en trouvent satisfaits.

Bibliographie

Bessis, D. (2022) Mathematica Seuil

Géninet, A. (2015) Faites-les réussir en maths Chronique sociale

Rigny, A. (2020) Apprendre à faire des maths avec plaisir et sans stress Eyrolles

Rigny, A. Faire des maths efficacement avec les cartes mentales (2021) Dunod

Sonnois , G. (2014) Accompagner le travail des adolescents avec la gestion mentale Chronique sociale