Tout d’abord, à tout seigneur tout honneur, le titre de mon article est clairement une référence au film Comment j’ai détesté les MATHS, d’Olivier Peyon, dont j’ai parlé dans un article précédent. Film que j’adore, qui m’a fait rire, m’a appris des choses et m’a fait beaucoup réfléchir. Je ne peux que vous engager à aller le voir !
J’ai cherché à me souvenir de « comment j’ai aimé les maths ». C’est pour moi une recherche difficile, parce que, paradoxalement, bien que les maths soient au cœur de ma vie professionnelle, je ne dirais pas spontanément que j’aime les maths. C’est plutôt les maths qui m’aiment. Plus précisément, j’ai toujours été « bonne en maths ».
Dans le film d’Olivier Peyon, on commence par une remise en cause des « maths modernes », réforme mise en place dans l’enseignement des mathématiques, dans les année 70. Cette réforme a été mal vécue, globalement, par tout le monde, y compris les enseignants. Pour autant, j’en ai de très bons souvenirs en tant qu’élève.
Je me rappelle notamment, et je pense que c’est mon premier souvenir mathématique, avoir appris à compter dans différentes bases : en base 2, en base 3, et dans une base quelconque.
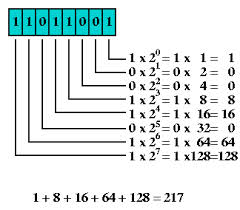
Concrètement, en base 2 par exemple, on dessinait des bâtons, puis on faisait des paquets de deux bâtons, on notait le nombre qu’il restait de bâtons (0 ou 1) puis des paquets de deux paquets, on notait à gauche du premier chiffre combien il en restait (0 ou 1), et ainsi de suite.
Par exemple, 10101 représente le nombre [math] 1\times 2^4+0\times 2^3 +1\times 2^2+0\times 2^1+1\times 2^0 [/math] c’est-à-dire 16+4+1=21.
Un autre exemple:
Je trouvais ça très amusant. Je trouvais également cela très lumineux et je crois que cela m’a permis de comprendre la numération de position en base 10 communément utilisée. Difficile de dire après tout ce temps si c’est un souvenir réel ou reconstruit, mais je daterais quand même mon intérêt pour les maths de cette époque. Je crois que ce que j’ai particulièrement apprécié, c’est la manière très concrète dont on nous faisait pratiquer : entourer des bâtons par paquets. Je ressentais les maths dans mon corps. (Je trouve cela dommage d’empêcher les enfants de compter sur leurs doigts, pour certains c’est crucial d’avoir une approche kinesthésique des nombres).
A contrario, les problèmes plus « traditionnels » de trains qui se croisent ou de robinets qui fuient, encore maintenant m’horripilent. Je les trouve faussement concrets, totalement artificiels.
Ce qui me plait dans cette histoire de bases, c’est le sentiment que plusieurs mondes existent, pas uniquement le monde connu de la base dix. De s’apercevoir que tout est une question de points de vue. Je ne dis pas du tout que c’est souhaitable d’enseigner les maths comme cela, simplement moi ça m’a plu.
Ce qui m’amuse encore plus, c’est que finalement, la base 2 est devenue fondamentale dans le monde actuel : en effet, le langage dans lequel sont écrits tous les programmes informatiques qui régissent nos vies quotidiennes, sont écrits en base 2. En base 2, il n’y a que deux symboles, 0 ou 1, impulsion électrique ou pas. Et avec ces deux symboles, on écrit le monde !
Une autre chose qui m’a fait aimer les maths, c’est la découverte de l’infini. J’en ai déjà parlé dans un article précédent.
Ce que j’aime dans les maths, c’est le côté incongru, inattendu. Dans le film d’Olivier Peyon, un jeune mathématicien explique ses travaux de recherche : il s’intéresse à la façon dont les spaghettis se disposent dans l’assiette quand on les fait tomber de la casserole : ils font des tours, des nœuds, ou tombent en ligne droite, etc. Là on se dit, « ok, il est gentil, on va encore prendre les mathématiciens pour des fous ». Et puis, il nous explique que tous les échanges d’informations, qui sont au passage rappelons-le, des échanges codés en 0 et 1, circulent d’un pays à l’autre par des gros tuyaux, qui passent dans les océans, tuyaux qui sont largués par bateau et vont se poser au fond de l’océan. Et c’est ennuyeux s’ils font des nœuds, ou s’ils ont trop tendus, etc. Et là, on se dit qu’en effet, les spaghettis, c’est un bon modèle, et que ces problèmes de tuyaux, c’est vraiment fondamental. On rigole déjà moins. J’avoue avoir été bluffée en regardant le film.
Je trouve ça intrigant quand une découverte mathématique a une application imprévue des années, voire des siècles plus tard. C’est le cas des nombres complexes, qui ont été inventés au 16ème siècle pour résoudre des équations du troisième degré, (du genre [math]2x^3+4x^2-5x+1=0[/math]), et qui se sont révélés cruciaux pour le développement de l’électricité et le traitement du signal (propagation du son par exemple) fin 19ème, début 20ème.
Ce qui me fascine également, c’est quand les maths se retrouvent dans la nature. Je passerai sur le cas du nombre d’or, il y a une abondante littérature à son sujet. Le nombre Pi également, qui représente la longueur d’un demi-cercle de rayon 1, très facile à obtenir, à toucher. (Quand on dit que les maths c’est abstrait….Pourtant on utilise des cercles tous les jours en payant son pain avec des pièces par exemple, donc on « voit » le nombre Pi tous les jours.)
Je voudrais m’intéresser à un phénomène sur lequel il n’existe pas, à ma connaissance d’explications. Il s’agit des nombres, en particulier des nombres premiers. Les nombres entiers, 1,2,3,4, etc. servent à compter. Certains visualisent facilement les nombres et les manipulent avec aisance. D’autres ne les visualisent pas du tout, ou alors cela dépend des quantités. Par exemple je me représente assez bien les nombres inférieurs à mille, j’arrive à voir ce que représente 100 000, mais déjà pour un million, je n’ai plus de repères. Parmi les nombres, certains sont dits « premiers ». Il s’agit de 2,3,5,7,11,13,17,19, etc., c’est-à-dire les nombres qui n’ont pas d’autres diviseurs que 1 ou eux-mêmes. (Impossible de partager 19 bonbons de manière équitable, sauf si on les partage entre 19 enfants). Au sujet des nombres premiers en eux-mêmes, il y a plein de choses fascinantes, d’ordre mathématique. (Entre autres, il y a une infinité des nombres premiers, mais on n’a pas de « formule » qui permet de donner un nombre premier de rang donné, qui pourrait donner le 56789432145676ème nombre premier par exemple. Ou encore, bien qu’on sache qu’ils se raréfient, il y a quand même une infinité de nombres premiers « jumeaux », comme 11 et 13 par exemple -c’est à dire de la forme n, n+2. Il y a également une suite de nombres aussi grande que l’on veut dans laquelle il n’y aura aucun nombre premier. Pour représenter les phénomènes de répartition des nombres premiers, on peut considérer la spirale d’Ulam.)
Mais, pourquoi, dans le cerveau des autistes en particulier, les nombres premiers apparaissent-ils différemment des autres ? J’ai lu une histoire à propos de jumeaux autistes, racontées par Oliver Sacks, (dans l’Homme qui prenait sa femme pour un chapeau je crois), ces deux frères communiquaient par « nombres premiers interposés ». 
Oliver Sacks raconte les avoir vu se murmurer des mots qu’il ne comprenait pas. Il se rend compte ensuite qu’il s’agit nombres. Un des deux dit un nombre, l’autre réfléchit, son visage s’éclaire et il lui répond par un autre nombre plus grand. Oliver Sacks se rend compte qu’il s’agit de nombres premiers. Il va chercher un livre dans lequel sont répertoriés des nombres premiers et se met à « jouer » avec eux. (Enfin, lui, il triche…). Ils expliquent ensuite plus tard à Oliver Sacks qu’ils voient les nombres premiers différemment des autres. Les nombres sont dans un paysage mental, et les nombres premiers apparaissent différemment. Mythe ? Ce qu’il faut savoir, c’est que déterminer si un nombre est un nombre premier est un problème mathématique assez long à résoudre (en gros il faut tester tous les diviseurs).. C’est d’ailleurs un enjeu de trouver des nombres premiers de plus en plus grand. On s’en sert dans les codes secrets.
Quoiqu’il en soit, le fait de « voir » les nombres dans sa tête est déjà assez fascinant. (Daniel Tammet explique très bien ce phénomème. Voir ici)
Pour finir, une chose qui me plait particulièrement, c’est que « nous sommes tous frères », et les maths le prouvent ! C’est un argument très simple, qui était utilisé dans une exposition au musée de l’Homme, il y a longtemps, ça pourrait être « Tous parents tous différents » dont voici la belle affiche, mais peu importe (je ne suis pas certaine que ce soit celle-là).
On va faire une démonstration par l’absurde. Prenons deux personnes, vous et moi par exemple. Imaginons que nous n’ayons aucun ancêtre commun. J’ai deux parents. Ils ont chacun deux parents, soit [math]2^2=4[/math] personnes à la deuxième génération avant moi. A chaque génération je multiplie par deux le nombre de mes ancêtres. A la génération n, j’ai donc [math]2^n[/math] ancêtres. Vous aussi. Si nous n’avons aucun ancêtre commun, il y a donc [math]2^n+2^n[/math]personnes différentes sur terre à la génération n. Pour simplifier, admettons qu’une génération dure 25 ans. Il y a 100 ans, soit 4 générations au-dessus, il y avait donc [math]2^4+2^4[/math] personnes distinctes sur terre (au moins) vos ancêtres et les miens. C’est-à-dire 32 personnes. Jusque-là pas de souci. 30 générations au-dessus (c’est-à-dire il y a 750 ans), il y avait donc [math]2^{30}+2^{30}[/math]personnes différentes sur terre (au moins), c’est-à-dire 2 147 483 648, c’est-à-dire plus de deux milliards d’individus. Or, la population mondiale est estimée entre 400 et 416 millions en 1250. Source Wikipedia
On aboutit donc à une contradiction (c’est le principe de la démonstration par l’absurde).
Résultat des courses, il est impossible que nous n’ayons pas d’ancêtres communs, nous sommes donc « frères ». (Au passage, on voit ce que cela veut dire « croissance exponentielle »).
Pour ma part, je trouve ça très beau, et très réconfortant.