Ce qu’on entend sur les maths
On entend des choses paradoxales sur les maths. Et parfois ce sont les mêmes personnes qui le disent.
- Les maths c’est difficile, c’est abstrait, c’est compliqué.
- Les maths ça ne me servira à rien, c’est loin de mes préoccupations.
- Les maths ce n’est pas intéressant, c’est toujours les mêmes exercices.
- Les maths c’est du calcul et comme il y a des machines, ça ne sert à rien d’apprendre à calculer.
- Les maths sont partout.
Mais si les maths sont partout, comment cela se fait-il qu’on les trouve si abstraites, si loin de « la vraie vie »?
Qu’est-ce qu’on entend alors par « faire des maths »?
Est-ce que quand on dessine des figures géométriques on fait des maths? Quand on fait des calculs? Quand on réfléchit à ses achats avec l’argent gagné? Quand on téléphone? Quand on joue aux échecs, quand on construit un meuble Ikéa?
Est-ce que « faire des maths » c’est uniquement en cours de maths? Quand on résout un exercice?
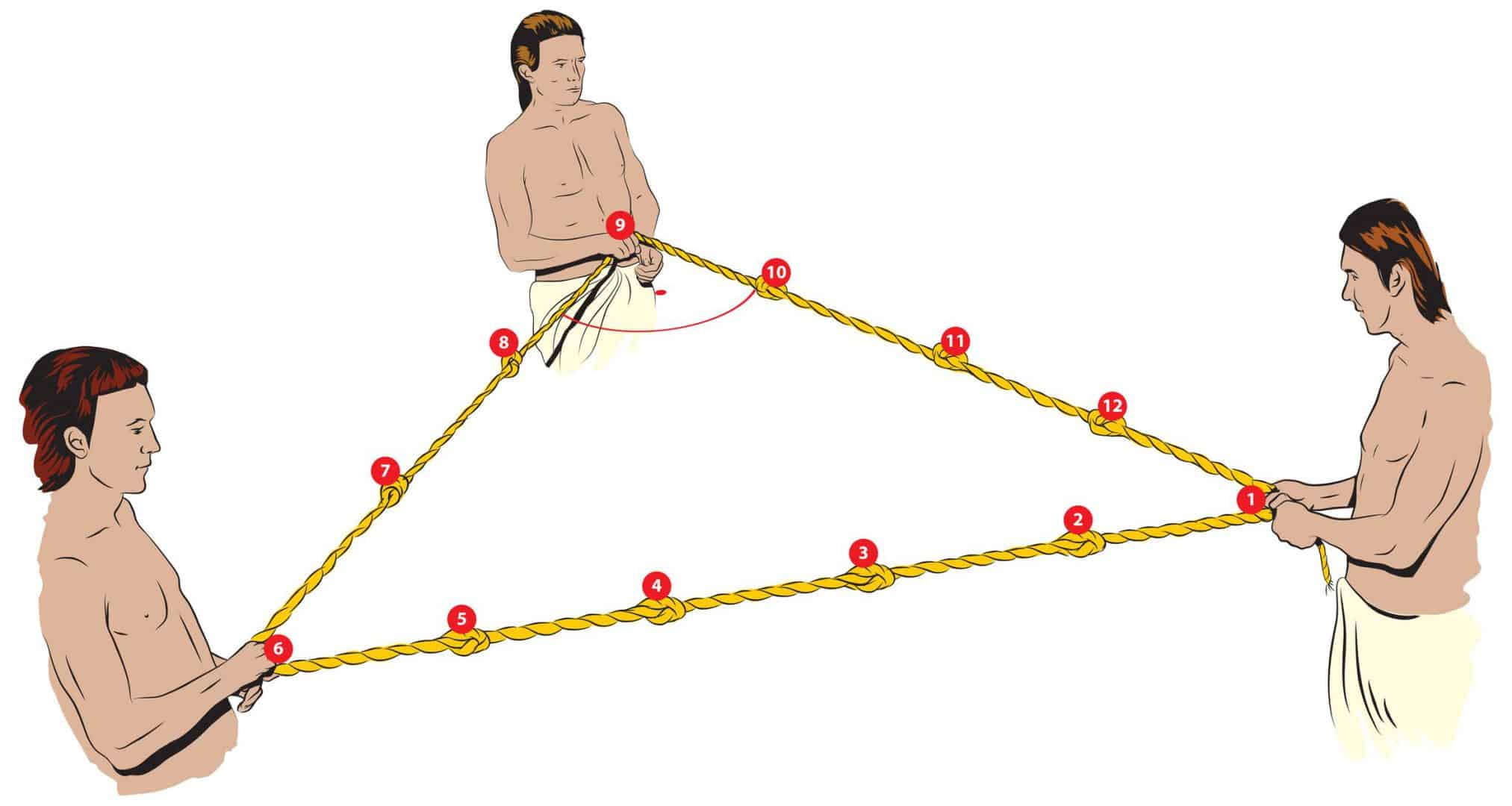
Est-ce qu’on a besoin de comprendre les théorèmes pour les utiliser? (Par exemple pour faire un angle droit avec une corde à nœuds, est-ce qu’il faut connaître le théorème de Pythagore?)
Est-ce que c’est plus simple de comprendre un exercice qui raconte une histoire ou avec des lettres?
La formulation de l’exercice
- A est une partie de E, nA est l’effectif de A et nE l’effectif de E et p la proportion de A dans E. Calculer p lorsque nA=873 et n3=3600″ (exercice tiré de Indice maths 2de chez Bordas Editeur).
- Dans le lycée il y a 3600 élèves dont 873 en seconde. Calculer la proportion d’élèves de seconde dans le lycée.
Lequel de ceux deux exercices préférez-vous? Ces deux exercices utilisent exactement les mêmes notions mathématiques et nécessitent pour y répondre de faire le même calcul.
Quand j’étais jeune, j’ai eu la chance de « faire des maths modernes ». Fini les problèmes de baignoires qui se vident, de trains qui se croisent, etc. Toutes choses que je trouvais prodigieusement ennuyeuses. Vivent le diagrammes de Venn et les décompositions des nombres en base !
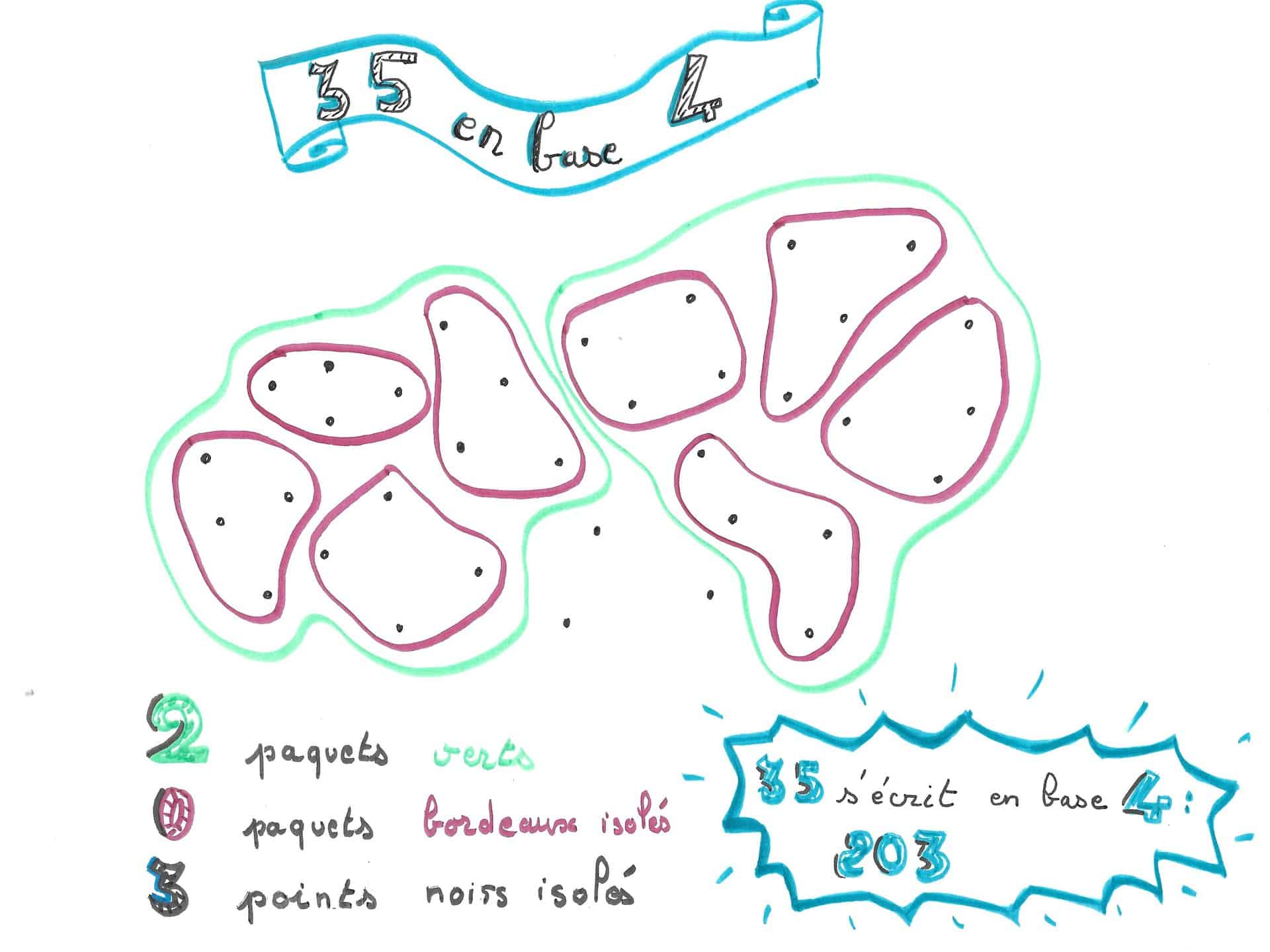
En fait c’était très concret. On dessinait des points sur la feuille, on faisait des paquets de 4, on comptait combien il en restait « tous seuls », puis on faisait des paquets de paquets de 4, on comptait combien il y en restait, et ainsi de suite.
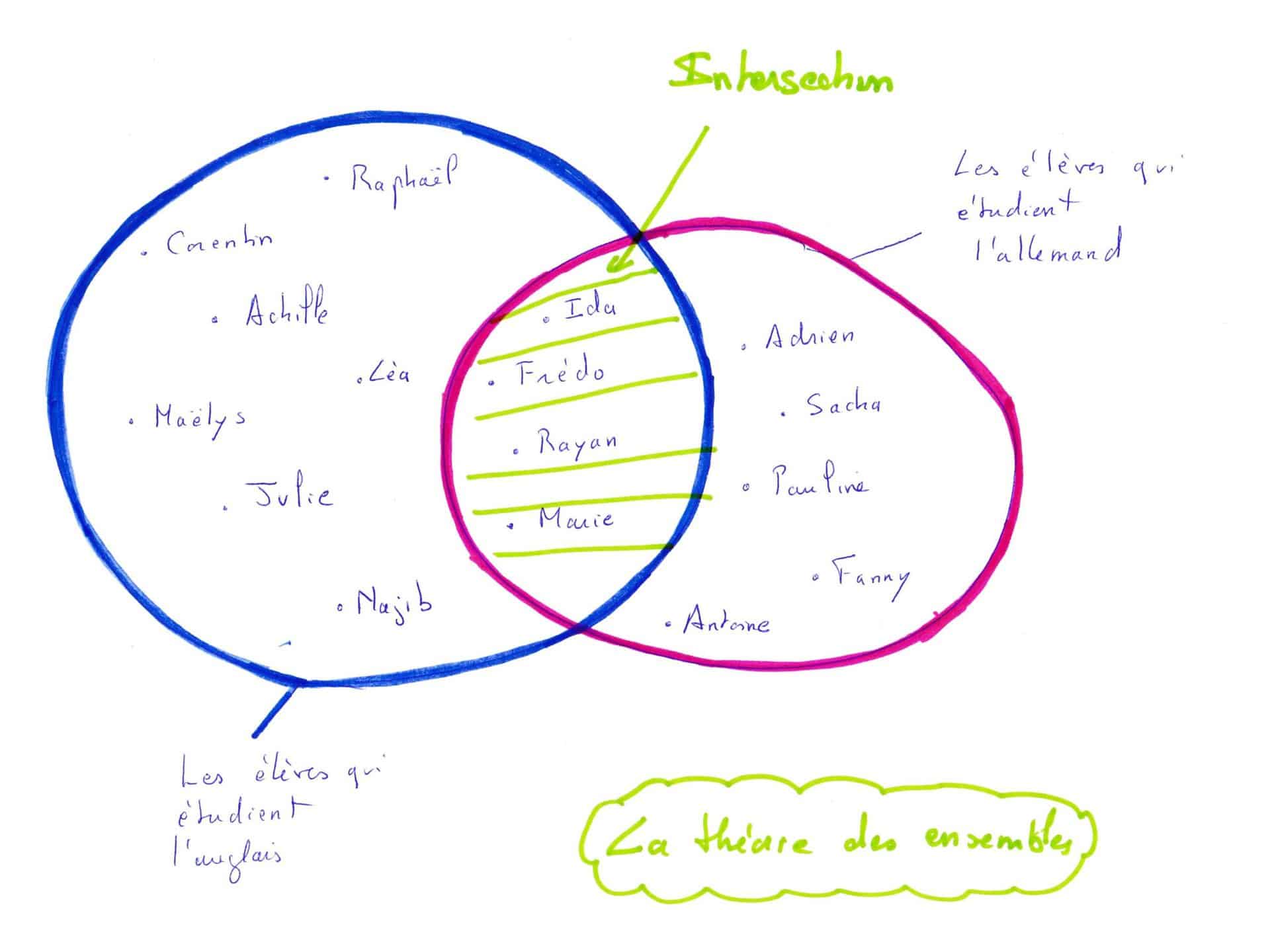
Les diagrammes de Venn, ou « les patates », c’est une représentation symbolique des ensembles. En fait, on dessinait beaucoup, c’était marrant.
Voilà une illustration de la notion d’intersection d’ensembles :
Comment rendre les maths plus concrètes?
La méthode Singapour
On a beaucoup parlé de la méthode Singapour, qui est considérée comme une méthode efficace pour apprendre les mathématiques. En tout cas, il est indéniable que dans les tests internationaux de niveau en mathématiques, les petits singapouriens s’en sortent beaucoup mieux que les petits français. Voir les résultats de l’enquête ici.
Alors de quoi s’agit-il ? C’est ce qu’on appelle l’approche « concrète-imagée-abstraite ».
Les élèves vont passer du monde concret qui leur est familier à une vision abstraite. Voici donc la démarche de la méthode de Singapour :
- Les élèves sont d’abord confrontés aux notions mathématiques par la manipulation d’objets. (Par exemple, ils vont apprendre l’addition en manipulant des cubes ou des jetons). C’est l’étape concrète.
- Ensuite, les objets sont remplacés par des images qui les représentent. Ainsi, une pile de dix cubes représentent le nombre dix, puis une pièce de dix centimes, etc. C’est l’étape imagée.
- Enfin, lorsque les élèves se sont familiarisés avec les concepts de la leçon, ils ne travaillent plus qu’à l’aide de chiffres et de symboles. C’est l’étape abstraite.
Cela est assez proche de la méthode Montessori. Avant tout, on fait manipuler les élèves (des bâtons, des cubes, etc.). On propose également de nombreux problèmes à résoudre, et on propose aux élèves de modéliser leurs problèmes.
Partager 35 bonbons entre 4 copains : dessiner les bonbons, ou prendre vraiment des bonbons, chercher comment en donner le même nombre à chaque enfant (un par un, ou deux par deux, ou..)
C’est également une approche « en spirale ». On étudie dès le CP les 4 opérations, et on y revient chaque année, en complexifiant.
La méthode heuristique
C’est une méthode d’enseignement des mathématiques à l’école primaire créée par Nicolas Pinel, professeur des écoles, conseiller pédagogique et inspecteur.
Elle repose sur 5 principes :
- Avoir une culture mathématique positive
- Répondre aux besoins des élèves
- Créer un environnement adapté
- Connecter les maths au monde
- Manipuler pour conceptualiser
Voir ici pour plus de détails.
Une des façons de connecter les maths au monde, est la promenade mathématique. Il s’agit de sortir, dans la rue ou dans la nature et de collecter tout ce qui est mathématique, par des photos par exemple et d’en parler en classe.
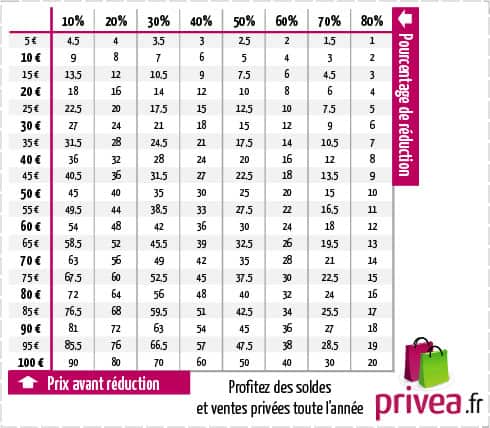
On peut facilement faire cela avec ses enfants. Il suffit de prêter attention à tout ce qu’il y a de mathématiques. Les chiffres bien sûr, les prix, les réductions, les poids sur les denrées alimentaires, les pourcentages dans la composition, découper une tarte, un gâteau en parts égales, comparer des quantités, payer, rendre la monnaie, discuter des chiffres du covid19, etc., mais aussi des formes géométriques, des symétries, des frises, de tout ce qui présente une certaine régularité. (Ce qui est chaotique peut aussi se modéliser mathématiquement… mais c’est plus compliqué.).
Voici quelques exemples :





La beauté des formes géométriques
On peut sensibiliser les jeunes aux mathématiques par la géométrie. D’ailleurs souvent, au collège et à l’école primaire, les enfants préfèrent la géométrie, parce que c’est visuel justement. proposer des activités créatives à partir de formes géométriques, ou faire retrouver des formes géométriques dans des tableaux (trouver des spirales d’or, ou des proportions avec le nombre d’or), ou faire découvrir la perspective, tout cela sont des activités qui familiarisent avec les mathématiques, qui permettent d’associer maths et créativité, et de « faire des maths autrement ».
Quand on cherche à reproduire ou créer une figure, on se pose des questions mathématiques, indéniablement.

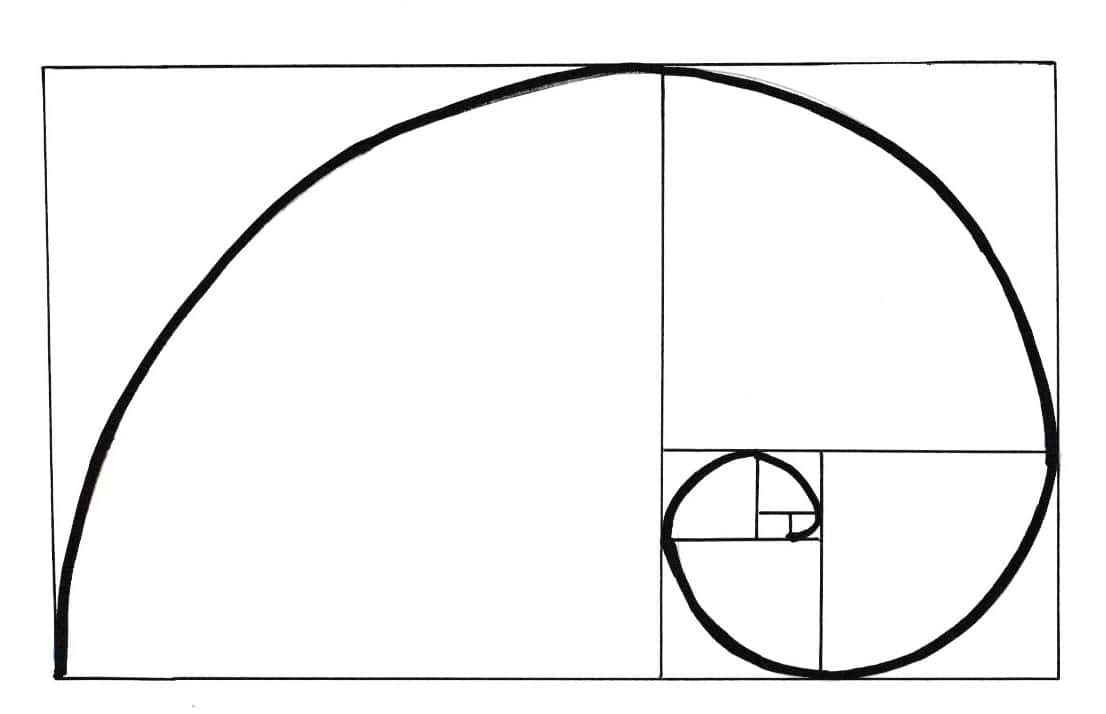
Une spirale construite à partir des rectangles d’or
La beauté des formules
Sofia Kovaleskaya, grande mathématicienne russe, née en 1850 à Moscou, et morte en 1891 d’une pneumonie, première femme a avoir eu une chaire universitaire, à Stockholm en 1884 et également écrivain, aventurière, a écrit dans ses souvenirs : « lorsque, pour la première fois nous nous installâmes à la campagne, il fallut réparer toute la maison, et mettre de nouvelles tentures dans toutes les chambres et elles étaient en si grand nombre que le papier manqua pour une de celles destinées aux enfants. […] la chambre resta inachevée, le mur simplement tendu d’un papier. Par un heureux hasard, ce papier consistait en feuilles lithographiées des cours d’Ostrogradski sur le calcul intégral et différentiel, jadis achetées par mon père dans sa jeunesse. […] Je me rappelle avoir passé des heures entières dans mon enfance, devant ce mur mystérieux, cherchant à déchiffrer quelques phrases isolées et à retrouver l’ordre dans lequel ces feuilles devaient se suivre. Cette contemplation prolongée et quotidienne finit par graver dans ma mémoire l’aspect matériel de beaucoup de ces formules, et le texte, quoique incompréhensible au moment même, laissa une trace profonde dans mon cerveau ».
Extrait tiré du livre de Michèle Audin, Souvenirs sur Sofia Kovalevskaya, chez Calvage et Mounet.
Denis Favennec raconte également dans cet article comment, enfant, il lisait dans l’Encyclopédia Universalis des articles de mathématiques sans y comprendre grand chose, mais fasciné par la beauté des dessins et des formules.
Pourquoi ne pas tapisser les salles de classes de formules mathématiques? Pourquoi ne pas apprendre aux élèves à tracer des symboles mathématiques, au moment où on leur apprend à tracer des lettres? Faire des dessins illustrant des formules? Raconter des histoires dont les personnages seraient des symboles mathématiques? Cela permettrait de s’approprier l’écriture mathématique dès le plus jeune âge de mêler des chiffres et des lettres, de se familiariser avec ce monde. Souvent, au collège, les élèves décrochent avec le calcul littéral. Quand les lettres s’associent aux maths, « alors là, je n’y comprend rien! « .
Voici un exemple de poème illustré de symboles mathématiques réalisé par un élève de primaire lors du festival des maths en scène en 2019. Voir mon article de mars 2019 pour plus de dessins.

Vous pouvez télécharger gratuitement ici le recueil de textes et dessins de formules en collaboration avec Emmanuel Amiot.

Susciter l’étonnement
L’étonnement est une bonne motivation pour apprendre. Quand est-ce que deux droites parallèles se recoupent?

Est-ce que la suite des nombres s’arrête? Pourquoi y -a-t-il deux fois moins de nombres pairs et pourtant le même nombre? Les mathématiques sont une source d’étonnement, d’émerveillement. Proposer des questions, des énigmes, des paradoxes, pour éveiller la curiosité.