D’une manière générale, faire une carte mentale est très aidant pour l’apprentissage, et pour l’apprentissage des maths en particulier. Les blocages en maths viennent souvent du fait que les élèves ne se posent pas les bonnes questions, voire ne se posent pas de question du tout.
Or se poser des questions, c’est la base !
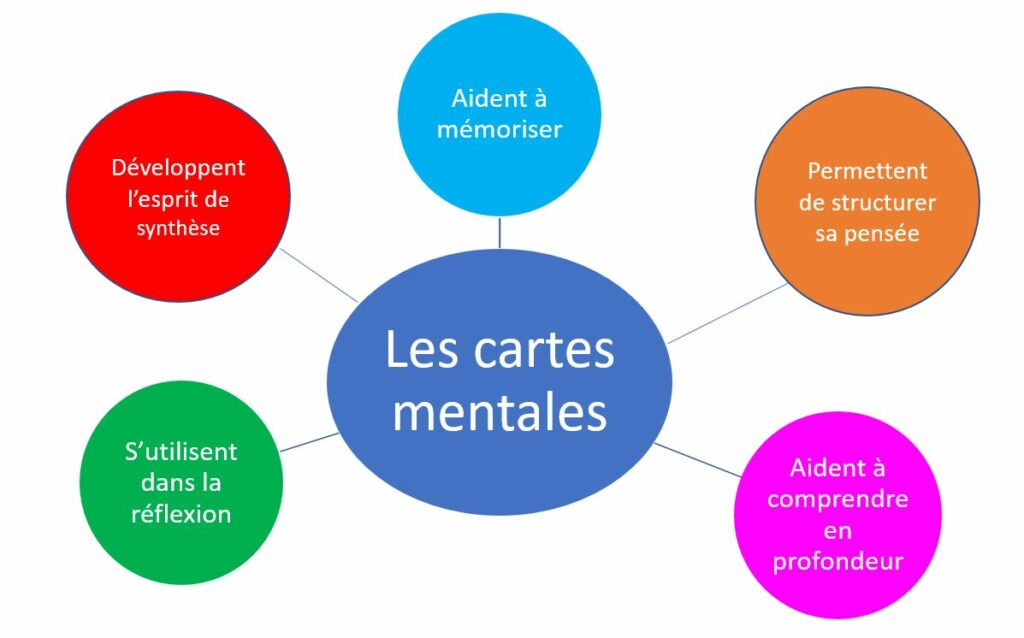
Les bienfaits des cartes mentales :
- Compréhension : on se pose des questions pour la construire
- Mémorisation : transformer son cours permet de le retenir. De plus la spatialisation et les couleurs permettent d’ancrer les connaissances
- Réviser ses anciens cours : une fois par semaine, on recrée de mémoire une carte mentale d’un ancien chapitre, et on compare avec l’original
- Réfléchir : on va chercher les idées dans la carte mentale pour résoudre un exercice de maths
- Pour synthétiser et structurer sa pensée : on résume, on cherche les points importants, on structure en choisissant un ordre de présentation
Comment s’y prendre ?
Il y a plusieurs façons de faire une carte mentale en maths. C’est un point abordé dans l’accompagnement Maths Sans Stress.
Voici un exemple :
On va construire une carte mentale sur les fonctions affines. Pour cela, on choisit de répondre « aux 5 questions pour comprendre »
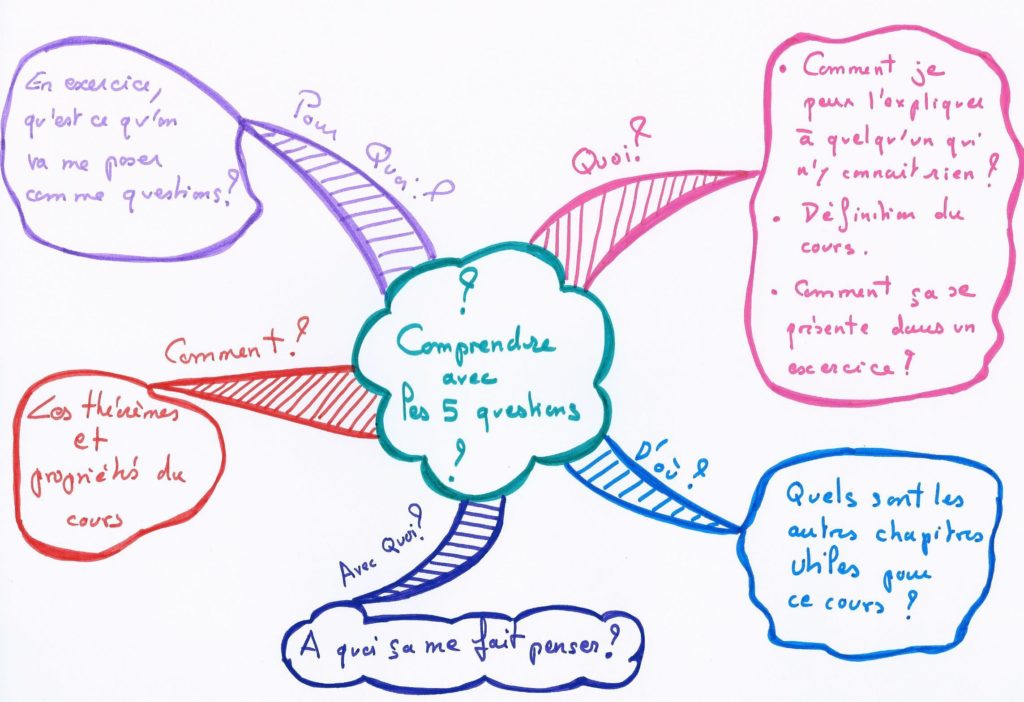
Quoi ?
De manière informelle, une fonction affine c’est « une droite ». La formule c’est mx+p.
Si on reprend la définition du cours, on remarque que « une fonction ce n’est pas une droite », mais la représentation graphique d’une fonction affine est une droite. Elle est définie par la formule f(x)=mx+p, où m est le coefficient directeur et p l’ordonnée à l’origine.
D’où ?
On observe ce qu’on utilise comme maths dans ce cours. Bien sûr on parle de fonctions, d’équations du premier degré, on fait des calculs, du calcul littéral.
Avec quoi ?
Cela dépend de chacun. Il se trouve que « affine » n’est pas un mot utilisé autrement qu’en maths (ce qui n’est pas le cas de fonction. « Je m’habille en fonction du temps » par exemple). En observant les exercices, les activités préliminaires, les dessins, on peut quand même penser à « proportion, droites, géométrie »
Comment ?
Ce sont les théorèmes et les propriétés du cours. Dans notre cas, comment calculer le coefficient directeur connaissant deux points, comment calculer p, quel est le tableau de variation.
Pour quoi ?
On peut y répondre en observant les exercices, et en cherchant les questions qui reviennent le plus souvent. Cette question permet aussi de se préparer pour les évaluations.
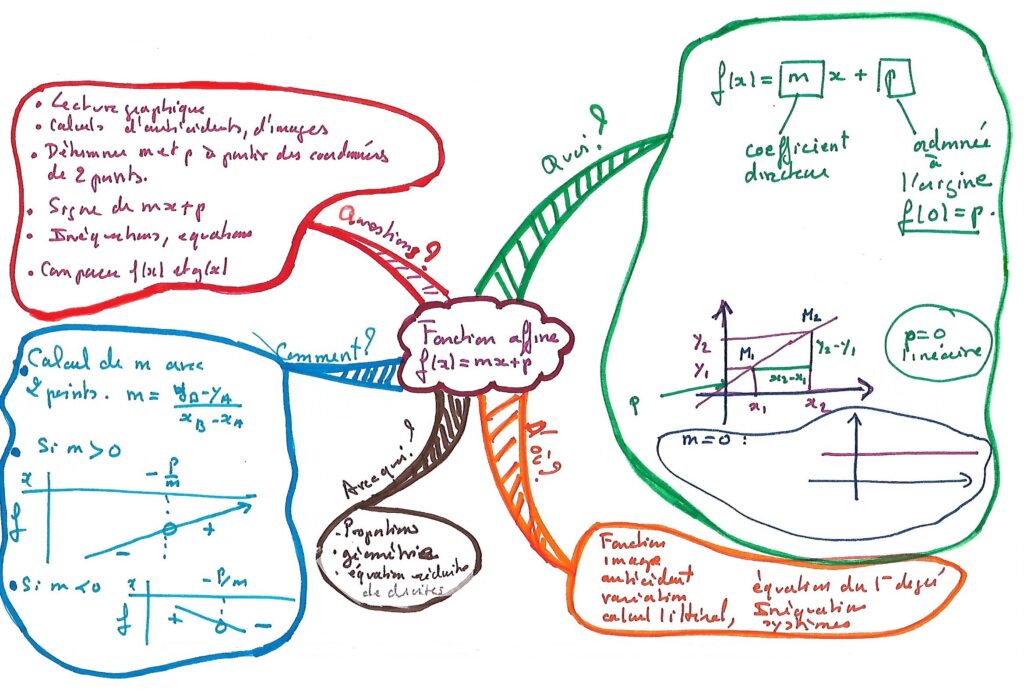
Ensuite, on note les informations dans la carte mentale. Il s’agit d’un résumé personnel, donc le formalisme du cours de maths n’est pas de mise. C’est quelque chose de personnel, de perfectible, qui évolue dans le temps. Cela peut -être judicieux de refaire une carte mentale sur le même thème quelques mois après.
Je conseille de faire les cartes mentales en format paysage (on a accès à toutes les informations d’un seul coup d’œil) et de les stocker dans des portes-vues.
Et de les utiliser pour résoudre des exercices !
Vous pouvez retrouver les cartes mentales des classes de seconde, première et terminale dans la boutique, et d’autres informations sur les cartes mentales ici.