Dans cet article, il est question de rêves, d’objectifs, du théorème de Fermat et d’Andrew Wiles et d’autres sujets passionnants.
On trouve moults articles sur les réseaux sociaux nous incitant à atteindre nos objectifs, à réaliser nos rêves, à « oser » être nous-même (en réalité comment faire autrement ?), à faire ce qui nous plaît (encore faut-il savoir ce qui nous plaît), et bien sûr on trouve de nombreuses propositions d’accompagnements pour cela. C’est d’ailleurs surprenant le nombre de personnes qui ont trouvé que ce qui leur plaît c’est accompagner les autres à trouver ce qui leur plaît. Si ces personnes accompagnées découvrent que ce qui leur plaît, c’est d’accompagner les autres à faire ce qui leur plaît… alors une récurrence vertigineuse s’amorce, ou une mise en abîme qui n’est pas sans évoquer la célèbre « vache qui rit ».
Il y a une citation attribué à Michel-Ange, « Le plus grand danger pour la plupart d’entre nous n’est pas que notre but soit trop élevé et que nous le manquions, mais qu’il soit trop bas et que nous l’atteignons « .
Andrew Wiles lui s’était choisi un but très très élevé. L’Everest des mathématiques. Il était tranquille pour le restant de ses jours, aucune chance de l’atteindre.
De quoi s’agit-il ? Il nous faut revenir au 17ème siècle, en Occitanie. Pierre de Fermat est un magistrat de la ville de Castres, puis de Toulouse. Mais il est surtout « polymathe », ce qui veut dire qu’il a des connaissances approfondies dans plusieurs domaines. Ses domaines de prédilection sont les mathématiques, le latin, le grec, la physique. Il est également poète. Bref, comme on dirait aujourd’hui, un haut potentiel. (Était-il également hypersensible ? L’histoire ne nous le dit pas.) A cette époque les « amateurs » pesaient dans le jeu autant que les professionnels. La profession ne définissait pas l’individu comme aujourd’hui, les frontières entre mathématiciens professionnels et amateurs étaient floues, en fait il y avait des personnes qui s’intéressaient aux maths et aux sciences, et Fermat était très écouté dans le milieu scientifique. On l’a surnommé « le prince des amateurs », (tandis que Gauss est surnommé « le prince des mathématiciens » et Ada Lovelace « la princesse des parallélogrammes »… beaucoup de têtes couronnées dans ce monde).
Fermat est en particulier pointu en théorie des nombres et dans les équations diophantiennes (équations portant sur les nombres entiers). IL est connu pour deux théorèmes, « le petit théorème de Fermat », et « le dernier théorème de Fermat ».
Qu’est-ce qu’un théorème? C’est une proposition mathématique vraie et DEMONTREE. En effet une proposition mathématique peut être vraie « par définition », ce sont les axiomes, ou bien elles sont vraies parce qu’il existe une chaîne logique entre un axiome et la proposition. Dans ce cas on parlera de théorème. Mais la démonstration peut « exister » sans qu’on l’ait encore trouvée. Sinon, on n’est pas certain qu’elle soit vraie. Le fait de trouver une démonstration permet de dire que la proposition est un théorème, sinon, c’est une conjecture. Il y a de nombreuses conjectures actuellement, par exemple la conjecture de Goldbach, qui affirme que tout nombre entier pair supérieur à 3 peut s’écrire comme la somme de deux nombres premiers. elle a été formulée en 1742 par Christian Goldbach et c’est l’un des plus vieux problèmes non résolus des mathématiques.
Le dernier théorème de Fermat est resté une conjecture pendant plus de 300 ans ! On peut dire que Fermat en a donné du fil à retordre aux mathématiciens !
Que dit ce théorème ?
Pour comprendre l’énoncé de ce théorème, faisons un passage par le théorème de Pythagore. Ce théorème permet de caractériser les triangles rectangles et réciproquement, de calculer des longueur quand on sait que le triangle est rectangle. Cette propriété est utilisée depuis l’antiquité pour construire des angles droits par les maçons, en utilisant une corde à nœuds.
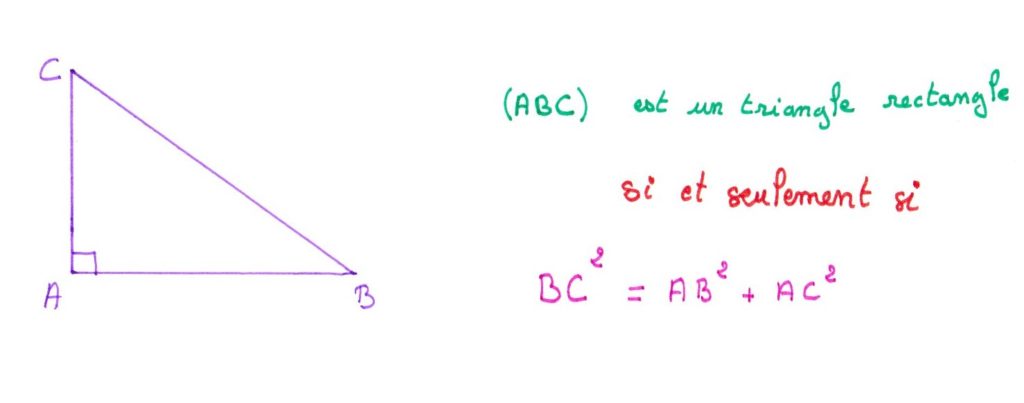
Par exemple, on a 3²+4²=5², donc on peut construire un triangle rectangle de côtés de longueur respective (3,4,5). On dira que (3,4,5) est un triplet pythagoricien.
Plus généralement, si x, y et z sont trois entiers, on dira que (x,y,z) est un triplet pythagoricien si et seulement si x²=y²+z².
La question que se pose Fermat en lisant une traduction des Arithmétiques de Diophante, c’est en quelque sorte une généralisation des triplets pythagoriciens. Peut-on trouver des triplets de nombres entiers non nuls (x,y,z) qui vérifient par exemple x3 + y3 = z3 ? Ou x4 + y4 = z4 ?
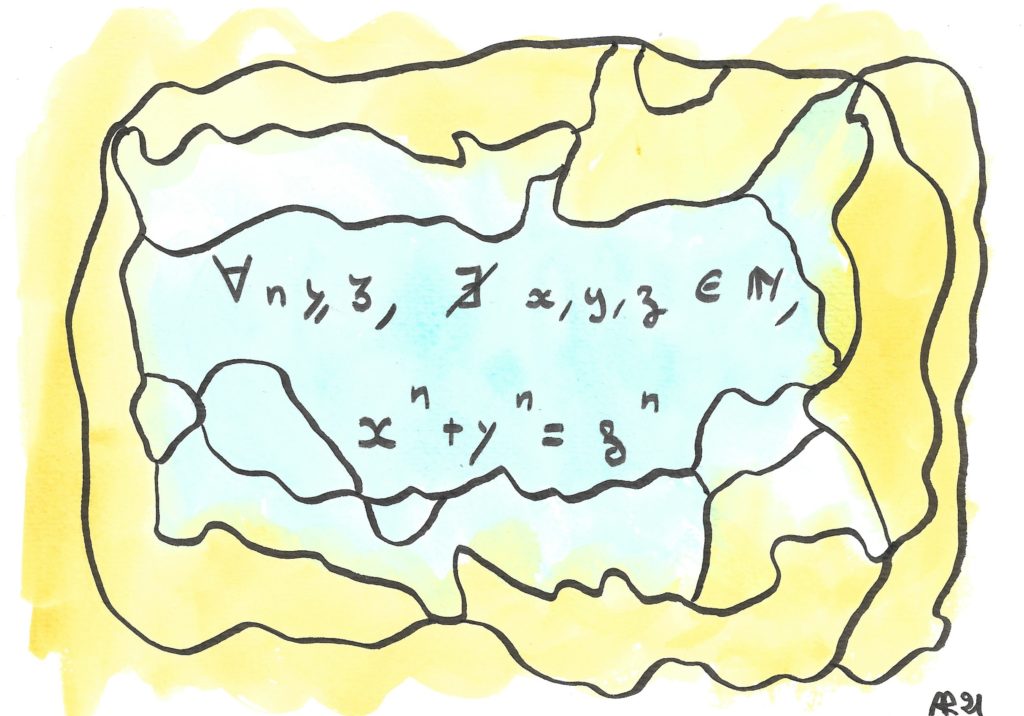
Ou plus généralement xn + yn = zn , pou n un entier supérieur ou égal à 3 ?
Il se pose la question, mais il y répond ! Dans la marge du livre, il écrit en substance « qu’il a trouvé une démonstration merveilleuse de ce résultat, mais qu’il n’a pas la place de l’écrire dans la marge de ce livre« . C’était en 1637.
Puis il est mort sans avoir donné sa démonstration. C’est seulement en 1670 que son fils retrouve le livre et l’annotation de son père et qu’il en fait part au public.
Démontrer cette conjecture est devenu une obsession pour beaucoup de mathématiciens, professionnel ou amateur. J’ai enseigné quelques temps au lycée Pierre de Fermat à Toulouse, et on recevait régulièrement des lettres d’amateurs de mathématiques (les professionnels ont d’autres canaux), proposant une démonstration de ce théorème. Le proviseur demandait alors aux professeurs de mathématiques leur avis.
La fièvre s’empare du monde des mathématiciens. L’académie des sciences de Paris, la société royale de Göttingen offrent des médailles et de l’argent.
Andrew Wiles est un anglais né en 1953. A l’âge de 10 ans, il découvre l’énoncé de la conjecture de Fermat. Il n’aura alors plus qu’un seul rêve en tête, démontrer cette conjecture. Pour cela, j’imagine qu’il a établi un plan d’action : devenir mathématicien professionnel avec la possibilité d’organiser son temps, avoir acquis suffisamment de connaissances en théorie des nombres, puis s’atteler à cette conjecture. En tout cas, c’est ce qu’il a fait. Après de brillantes études, il devient professeur à Princeton, une des plus prestigieuses universités américaines. L’Université de Princeton, c’est un peu le paradis des chercheurs. De nombreux mathématiciens y sont passés, comme élèves ou professeurs ou encore invités. On y trouve de grands noms, comme Albert Einstein, mais également Cédric Villani (une pointure en mathématiques avant de faire de la politique, avec moins de succès mais beaucoup de courage), Terence Tao y a étudié, également médaillé Fields comme Cédric Villani, Maryam Mirzakhani a également été professeure dans cette université, et médaillée Fields. Je n’ai pas fait de recherche plus approfondie, mais je me demande si tous les médaillés Fields n’ont pas, à un moment ou un autre, mis les pieds à Princeton. D’après mes informations (de seconde main, je n’y suis jamais allée), la vie là-bas est plutôt cool. Les professeurs sont assez libres de leur temps. Ils peuvent travailler tranquillement (surtout les mathématiciens, ils n’ont pas vraiment besoin de matériel autre que papier et crayon) ou bien partager leurs idées de façon très conviviale, autour d’un café, en se promenant dans les allées du parc.
Pendant huit ans, Andrew Wiles a donc travaillé, secrètement pour ne pas « se faire voler ses idées », sur la démonstration du théorème de Fermat. Pour être exact, il s’est attaqué à la démonstration de la conjecture de Shimura-Taniyama-Weil dont Kenneth Ribet a démontré en 1985 qu’elle était équivalente à la conjecture de Fermat. Il avait néanmoins mis un collègue dans la confidence, Nicolas Katz. Car, c’est souvent en discutant et en exposant clairement ses idées à quelqu’un qui comprend un peu que l’on avance dans sa réflexion. A ce niveau là, c’est quand même très difficile, et on n’est pas à l’abri de faire des erreurs que l’on n’arrive pas à détecter.
Quand Andrew Wiles a eu une démonstration qui tenait la route, pour l’expliquer et en même temps la faire vérifier, lui et Katz ont eu l’idée d’organiser un cours de doctorat ouvert aux étudiants et aux professeurs, intitulé « Calculs sur les courbes elliptiques ». On est loin du théorème de Fermat ! Lors de trois conférences (21,22 et 23 juin), sans en annoncer l’objet, Wiles présente ses résultats. A la fin de la troisième conférence, il annonce que la conjecture de Fermat est alors démontrée, comme corollaire de ses résultats. Coup de tonnerre dans le Landerneau des mathématiciens ! Il faut bien avoir en tête que la démonstration complète et rigoureuse fait plus de 100 pages. Pendant les conférences, il donne les grandes idées, mais ne peut pas rentrer dans tous les détails. Et pour qu’une démonstration de cette taille soit validée, la bonne foi du mathématicien ne suffit pas. Il faut qu’un nombre suffisamment élevé de mathématiciens suffisamment réputés la valide également.
C’est ce qu’il se passe aussi en classe. Si on pose une question, (par exemple le triangle ABC est-il rectangle ?) il ne suffit pas de répondre par oui ou non. Il faut proposer une démonstration, et qu’elle soit validée par le professeur en l’occurrence.
Dans le cas de la démonstration d’Andrew Wiles, le nombre de mathématiciens aptes à la valider n’est pas si élevé. Cependant, un mathématicien met en évidence une lacune dans sa démonstration. Pas une erreur, mais une étape non démontrée. Gros stress ! Andrew Wiles a dû y travailler une année supplémentaire, mais a finalement pu dépasser l’obstacle. La conjecture de Fermat est officiellement validée en octobre 1994 et prend le nom de théorème de Fermat-Wiles.
Andrew Wiles a donc mis à peu près trente ans pour réaliser son rêve. Pas mal. Il avait un tout petit peu plus que 40 ans et n’a donc pas pu obtenir la médaille Fields, mais sinon, tous les honneurs possibles et inimaginables lui sont tombés dessus. Il a reçu, vingt deux ans plus tard, en 2016, le prix Abel, accompagné de la somme de 620 000 euros (les récompenses de l’académie des sciences de Paris et de la société royale de Göttingen étaient expirées en 1994). Mais je ne pense pas que ça lui ait fait ni chaud, ni froid. A ce stade de passion et d’investissement, le moteur n’est pas l’argent.
La question que je me pose, c’est, « qu’a donc pu faire Andrew Wiles après ça ? ». D’où le thème de mon article. Qu’est-ce qu’on peut bien faire quand on a atteint son rêve, et un rêve de cette ampleur ? Je me souviens d’une interview dans le film de Simon Singh, Le dernier théorème de Fermat, avoir vu Wiles pleurer, non pas de joie, mais parce qu’il était perdu, désemparé. Quand à 40 ans, on vite le moment le plus important de sa vie professionnelle, qu’est-ce qu’il se passe après ?
La réponse est certainement différente pour chacun. Pour ma part, à 40 ans, j’avais atteint « le top » dans ma vie professionnelle de professeur de classes prépa. Je pouvais continuer à faire encore la même chose 25 ans. J’ai choisi de tout quitter pour me donner un nouveau challenge. C’est peut-être (mais c’est une pure supposition, je ne le connais pas personnellement) ce qu’a choisi de faire Cédric Villani après avoir obtenu sa médaille Fields. Il a choisi de faire de la politique, rien à voir avec les maths. En même temps, il était arrivé au sommet, que pouvait-il faire de mieux dans ce domaine ?
Je pense aussi au film d’animation « Le sommet des Dieux », film réalisé par Patrick Imbert, qui raconte l’histoire d’alpinistes voulant atteindre le sommet de l’Everest. Un des protagonistes dit à un moment, en substance « tu sais bien que le but ce n’est pas d’arriver au sommet. C’est autre chose« .
