Julia, élève de Terminale en spé Maths
Julia1 est une élève de Terminale. Elle a choisi la spécialité maths en première et l’a conservée en Terminale. Quand elle vient dans mon cabinet, elle est en perte de confiance. Elle ne comprend rien (sic), ne sait pas comment trouver les idées pour faire des exercices. Elle n’ose pas poser de questions en classe, son professeur de maths lui fait un peu peur. Il va très vite, et elle croit qu’il ne va pas apprécier si elle l’interrompt. Elle pense confusément que c’est « de sa faute » et que poser des questions ce serait remettre en cause les compétences de son professeur, passer pour une incapable aux yeux de ses camarades.
Lors du premier entretien, on a une conversation autour de ce ressenti à propos de son professeur. Pourquoi il lui fait peur, qu’est-ce qu’elle se raconte, etc. Je lui parle des 4 piliers de l’apprentissage de Stanislas Dehaene , en particulier de l’importance de l’engagement. Et l’engagement, cela commence par son attitude en cours. Venir avec le projet de comprendre, de poser des questions. On cherche des moyens de poser des questions qui ne la mettent pas mal à l’aise : par exemple se noter la question sur un papier et la poser au professeur à la fin du cours, ou pas, mais en tout cas la noter. Et puis on va regarder les fondements de sa croyance et traverser la peur de poser des questions à son professeur : qu’est-ce qu’il peut lui arriver si elle pose une question ?
Lors de cet entretien, on aborde aussi la question du calcul. Comment et pourquoi s’entraîner en calcul. On établit un programme quotidien de calcul, on part sur les fractions (ça ne fait jamais de mal de s’entraîner sur les fractions 🙂 ! )
Lors du deuxième entretien, on travaille autour des « 5 questions pour comprendre ».
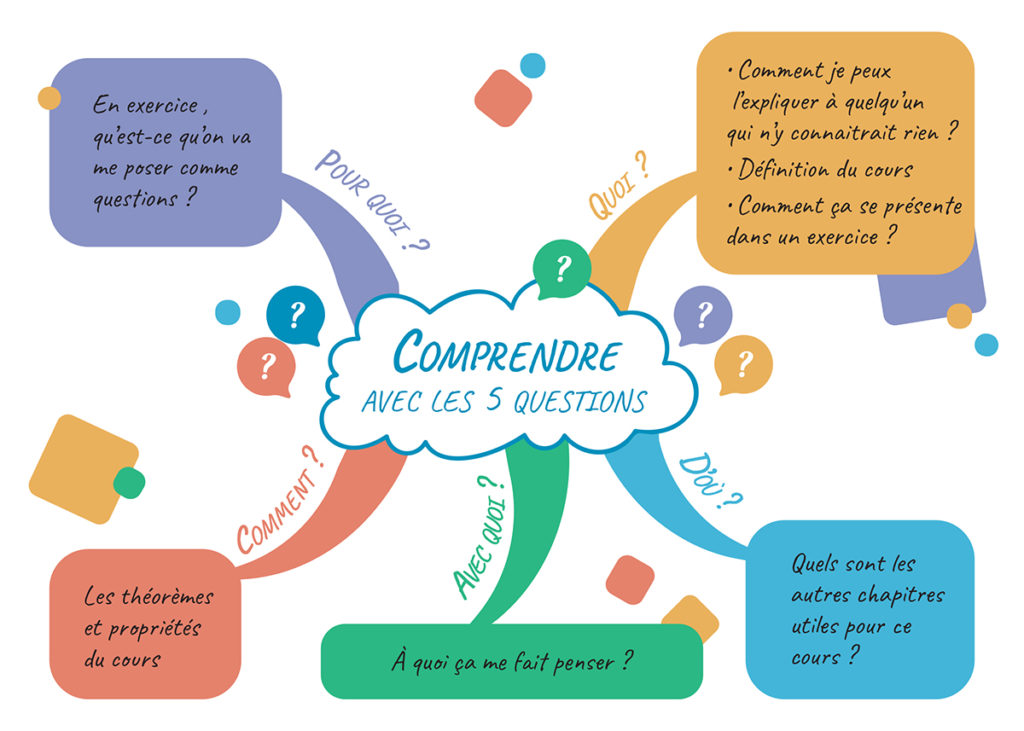
Il est important de faire la différence entre « comprendre » et « être familier ». Comprendre c’est beaucoup plus profond.
On balaye les différentes branches de la carte mentale, à partir de son cours sur le théorème des valeurs intermédiaires. On porte une attention à la branche « avec quoi ? ». Prendre l’habitude de faire des associations d’idées est très utile, en général, et en maths en particulier. Je lui dis en plaisantant qu’il n’y a que quand on enseigne quelque chose qu’on le comprend, et plus sérieusement, que ce serait profitable qu’elle travaille en binôme avec un camarade, à s’expliquer mutuellement le cours.
Pour le 3ème rendez-vous, Julia arrive radieuse. Elle s’est emparée et a mis en pratique tout ce que nous avons vu. Elle s’est intéressée au cours, a pensé à des questions, a écouté les questions posées par ses camarades, a osé posé des questions elle-même. Elle s’est rendue compte que son professeur « n’était pas si méchant ». Elle a mis en place de travailler les maths avec un camarade, ils s’expliquent le cours et s’interrogent mutuellement . Elle se sent déjà beaucoup plus à l’aise. Elle est contente aussi, parce que son professeur vient la voir pendant son cours, il s’intéresse à elle, gentiment. Elle n’a plus peur de lui. Un « cercle vertueux » se met en place.
Lors de ce troisième rendez-vous, nous détaillons ensemble le processus de réflexion, (comment on cherche un exercice) et également la bonne façon de rédiger.
Elle repart satisfaite de ses trois séances, qui lui ont permis de « désacraliser » les maths (ce sont ses propres mots) et de se rendre compte qu’elle pouvait y arriver.
1. le prénom a été volontairement modifié.