Et réciproquement, être testé négatif signifie-t-il ne pas être infecté ?
Tests et probabilités
En ce moment, tout le monde parle de tests, et tout le monde se fait tester. On a entendu parler de « faux positifs » et de « faux négatifs ». Et que penser du résultat d’un test ? Bien sûr cet article s’appuie sur l’actualité dominante en 2020, mais le raisonnement est valable pour n’importe quel type de tests (pour le test du SIDA par exemple), ou le dépistage de la trisomie 21 chez le fœtus. Ou encore le dépistage du cancer du sein. Egalement dans des situations moins polémiques telles que le « contrôle qualité ». Bref c’est une situation très fréquente.

Qu’est-ce qu’un faux positif ?
C’est quand le résultat du test est positif alors que la personne testée n’est pas infectée par le virus. Et un faux négatif, c’est quand le résultat du test est négatif alors que l’on est infecté. Il existe des tests fiables à 100%, comme une analyse de sang dans le cas qui nous intéresse, mais c’est un test long et coûteux, donc on propose d’abord un autre test. Il est plus rapide, moins coûteux, mais… moins fiable (on ne peut pas tout avoir).
J’ai trouvé dans un article du monde daté du 22 septembre 2020 les estimations concernant la fiabilité du test :
« Les tests PCR par voie nasale sont les plus fiables dont on dispose actuellement. Ils peuvent toutefois présenter une proportion de 30 % de faux négatifs lorsque le prélèvement est mal réalisé. Soit de manière trop superficielle, si l’écouvillon n’a pas été assez enfoncé, par exemple, soit si le dépistage a été fait au mauvais moment. Lorsqu’un malade est testé trop tôt (pendant la phase d’incubation) ou tout à la fin de la maladie, la quantité de virus peut être trop faible pour qu’il soit repéré. Le président du Syndicat des biologistes, François Blanchecotte, se montre rassurant : la sensibilité du test est de « 98 % quand on prélève correctement », a-t-il déclaré à l’AFP, tandis que Laurent Andreoletti, responsable d’une unité de diagnostic Covid-19, estime son taux de fiabilité de l’ordre de 80 à 90 %. »
Pour mon article je vais donc utiliser les chiffre de 98% de fiabilité pour le test positif, c’est à dire: si le patient est infecté, le test a 98% de chance d’être positif. Donc, il a 2% de chance d’être négatif. Je n’ai pas trouvé de données sur la fiabilité si le patient n’est pas malade, on va prendre les mêmes chiffres. Mais attention, la question n’est pas de savoir si le test est positif quand on est infecté, car si on sait qu’on l’est, on s’en moque un peu du test. La question est inverse: si le test est positif, est-ce que je suis infecté ? Comment calculer cette probabilité, car vous l’aurez compris, rien n’est sûr. Tout est probabiliste.
Interprétation mathématique
Là, on va faire un peu de maths, en utilisant deux formules : la formule des probabilités totales et la formule des probabilités conditionnelles.
Dans notre situation, 98% représente justement la probabilité d’être positif si on est infecté, c’est ce qu’on appelle la probabilité conditionnelle (sachant que j’ai des informations).
Petit aparté sur les probabilités conditionnelles: voilà un exemple plus simple. Vous êtes invité chez des amis, vous savez qu’ils ont deux enfants. Quelle est la probabilité qu’ils aient deux filles ? Il y a 4 situations possibles, ayant la même probabilité chacune (je fais l’hypothèse qu’il y a autant de chance d’avoir une fille qu’un garçon). FF,FG,GF,GG. (FF=fille ainée, fille cadette etc.) Donc la probabilité qu’ils aient deux filles est 0,25 (1 chance sur 4). Vous arrivez chez vos amis, et une petite fille ouvre la porte. Donc vous savez qu’ils ont au moins une fille. Quelle est la probabilité que l’autre soit une fille? Il n’y a plus que 3 cas possibles: FF, FG, GF. La probabilité est donc de 1/3, une chance sur 3. Si elle vous dit qu’elle est l’aînée, la probabilité que l’autre soit une fille devient 0,5, car il n’y a que deux cas : FG, FF.
La formule des probabilités conditionnelles
En maths ça s’écrit : P(I∩T)=P(I) × P(T/I).
Je m’explique : I c’est l’évènement « être infecté », T c’est l’évènement « être positif ». La formule se lit donc « la probabilité d’être infecté ET positif est le produit de la probabilité d’être infecté multiplié par la probabilité d’être positif SACHANT qu’on est infecté » – (Les maths c’est quand même plus concis…).
La formule des probabilités totales
En maths ça s’écrit : P(T)=P(T∩I)+P(T∩S), où S est l’évènement contraire de I, c’est à dire « être sain ».
En français ça se dit : la probabilité d’être positif c’est la somme de la probabilité d’être positif et infecté avec la probabilité d’être sain et positif. Voici un arbre de probabilité, qui résume la situation : (j’ai noté N l’évènement « être négatif »).
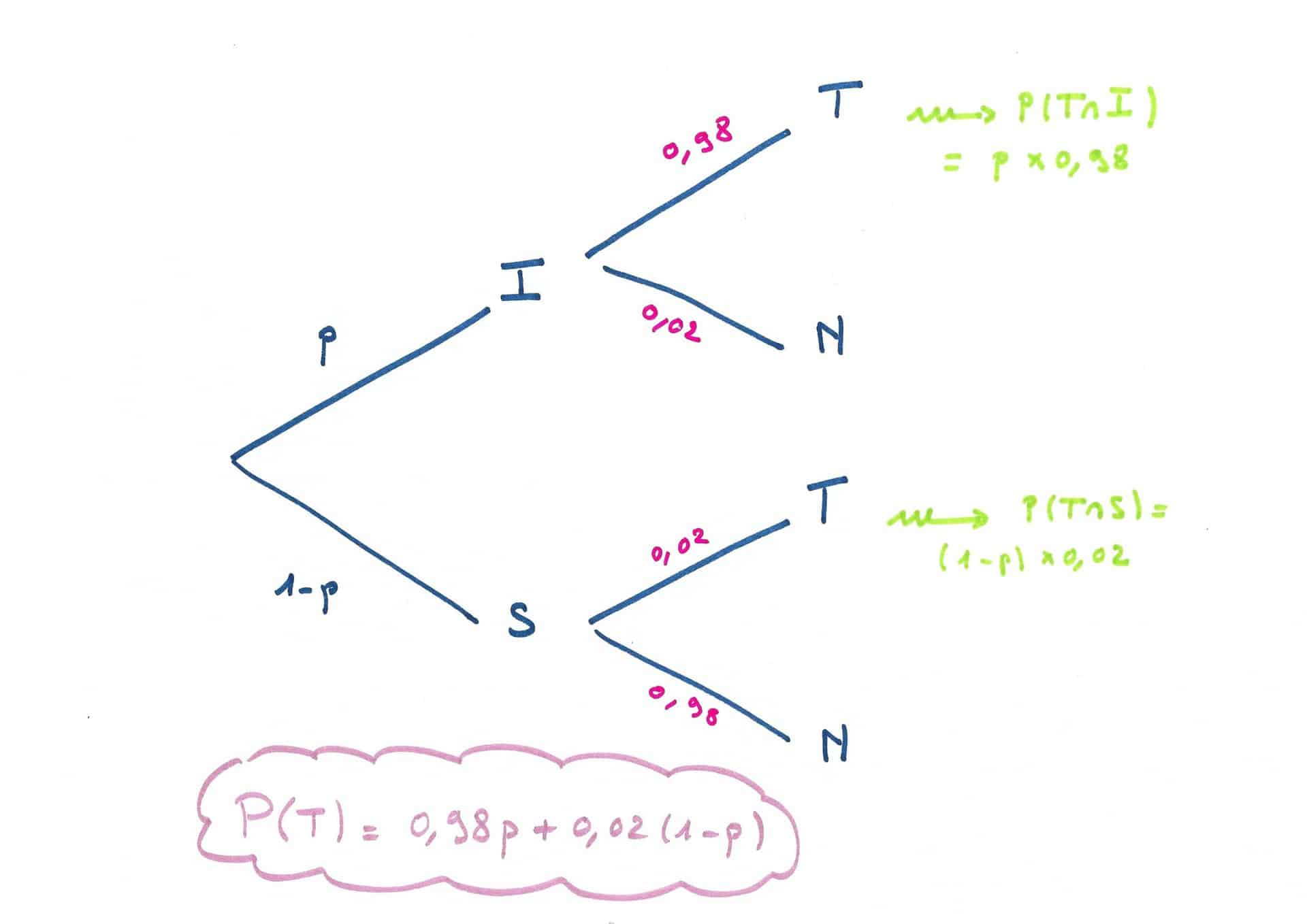
Il nous faut maintenant évaluer p, la probabilité d’être infecté. C’est à dire le pourcentage de personnes infectées dans la population. Evidemment, on ne connaît pas exactement ce chiffre. On va faire des estimations. On verra dans la troisième partie comment estimer ce chiffre. Pour nous faire une idée, j’utilise les chiffres du gouvernement .
Démonstration par le calcul
250 pour 100 000 habitants, est le taux d’alerte maximale, qui correspond aux nombres de cas « officiels » de covid 19. (Ce qui n’est pas clair c’est si c’est par jour ou depuis le début.)
Disons que cela fait 0,25 pour 100. On va donc faire les calculs avec cette estimation, qui est plutôt « haute ».
On a donc P(T)=0,25% ×0,98+0,02 × 99,75%= 0,0224 (2,24%)
P(T) = 2,24%, cela veut dire que, si on prend une personne au hasard dans la population et qu’on la teste, il y a 2,24% de chance que le résultat du test soit positif.
Mais ce qui nous intéresse, c’est la probabilité d’être infecté si notre test est positif, ce qui mathématiquement est la quantité P(I/T). Si on reprend la définition donnée plus haut, P(I/T)=P(I ∩ T)÷P(T) = 0,98 × 0,25% ÷ 0,0224= 0,109375. (A peu près 11%) .Ce qui veut dire, que dans ce cas, la probabilité d’être infecté quand le test est positif est d’un peu plus d’une chance sur 10.
Influence du taux de contamination de la population
Nous allons voir que cette probabilité évolue en fonction du taux de contamination dans la population. Supposons par exemple qu’une personne sur 10 soit infectée, ce qui représente 10%. On va refaire le calcul précédent avec cette nouvelle valeur de p. (p=0,1).
On obtient donc d’abord P(T)=10%×0,98+0,02 × 90% = 0,116 (11,6%),
puis P(I/T)=P(I ∩ T)÷P(T) = 0,98 × 10% ÷ 0,116 = 0,84.
On a donc cette fois à peu près 84% de chance d’être effectivement infecté si le test est positif.
À partir de quelle proportion d’infectés dans la population cette probabilité devient supérieure à 95% ? Pour cela, nous allons résoudre une inéquation.
On a P(T/I)=p × 0,98 ÷ (p×0,98+0,02 × (1-p)) (p étant le taux de contamination).
On souhaite donc résoudre l’inéquation : P(T/I) ≥ 0,95.
—
p × 0,98 ÷ (p×0,98+0,02 × (1-p))≥0,95
p × 0,98 ≥ 0,95 × (p×0,98+0,02 × (1-p))
On développe et on réduit,
p × 0,98 ≥ 0,95 × 0,98 ×p+ 0,95 × 0,02 – 0,95 ×0,02×p
p × 0,98 ≥ 0,912 × p+ 0,019
p ×(0,98-0,912) ≥ 0,019
p ×0,068 ≥ 0,019
p ≥ 0,019 ÷ 0,068
p ≥ 0,28
En d’autres termes, il faut un taux d’infection de 28% dans la population, pour que la probabilité d’être vraiment infecté sachant que l’on a un test positif soit supérieure à 95%.
Comment estimer le taux de contamination de la population?
C’est exactement la problématique des sondages pour une élection politique. On a trop tendance à oublier que les résultats d’un sondage d’une ne donnent qu’une réponse à l’instant où le sondage est fait, et que les résultats même du sondage vont avoir une influence sur la population. D’autre part un sondage ne donne qu’une « fourchette », et une probabilité.
Autrement dit si le sondage donne 51% au candidat A , sur un échantillon de 1000 personnes, cela veut dire: la probabilité que le résultat dans toute la population à cet instant soit situé entre 0,48 et 0,54 est supérieure à 0,95. (J’ai pris une formule approchée, mais ça ne change pas grand chose au résultat). Dans notre cas on voit que de toute façon, la victoire n’est pas assurée.
Avant de dire « les sondages mentent », ce serait bien de donner les résultats du sondage dans toute leur complexité.
Comment évaluer le taux de contamination de la population ?
Comme on ne peux pas tester tout le monde, on va choisir un échantillon, représentatif de la population générale. On a déjà une première difficulté : comment être quasi certain que l’échantillon est bien représentatif? Si on choisit 1000 personnes de moins de 20 ans, ou 1000 personnes de plus de 70 ans, dans les deux cas, l’échantillon ne sera pas représentatif.
Imaginons donc que l’on choisisse un échantillon représentatif de n personnes, et que la fréquence de résultats positifs soit de f. (Par exemple si n=1000, et qu’on a 51 cas positifs, f=51÷1000=0,051). Alors, nous pouvons dire qu’à 95%, le taux de résultats positifs dans la population globale se situe entre f-1/√n et f+1/√n, ce qui donnerait dans notre cas 0,051-0,03=0,021 et 0,051+0,03=0,081. On estime alors que P(T)=0,051.
Quelle est la valeur de p alors (rappelez-vous qu’il y a des faux positifs) ?
En reprenant la formule de la précédente partie, P(T)=p×0,98+0,02 × (1-p)) = 0,051.
On résout alors l’équation d’inconnue p, ce qui donne p=0,033, un taux de contamination de 33 pour 1000.
Aparté théorique: l’intervalle [f-1/√n , f+1/√n] s’appelle un intervalle de confiance. C’est l’intervalle dans lequel se situe p, avec 95% de chance. Plus d’informations sur les intervalles de confiance ici.
Conclusion
J’espère vous avoir apporté un éclairage sur tous les chiffres que nous avons chaque jour dans les médias. Il faut comprendre que à chaque fois, il s’agit d’estimation, de probabilité. Dans notre époque complexe, un bon niveau de mathématiques est indispensable pour comprendre et ne pas se faire manipuler. Les mathématiques utilisées ici sont du niveau de première. Malheureusement les mathématiques étant optionnelles à partir de la première, peu de personnes y ont accès au lycée.
