Ecrit par Stéphane Jaubert

Tout un programme ! 

« réconcilier tous les élèves » avec les mathématiques et « promouvoir l’égalité filles-garçons »

https://www.service-public.fr/particuliers/actualites/A16124

Objectifs ambitieux ? Sûrement !

Au-delà du débat sur le sujet, je vous propose dans cette série d’articles de regarder un peu plus en détail en quoi consiste ce programme.

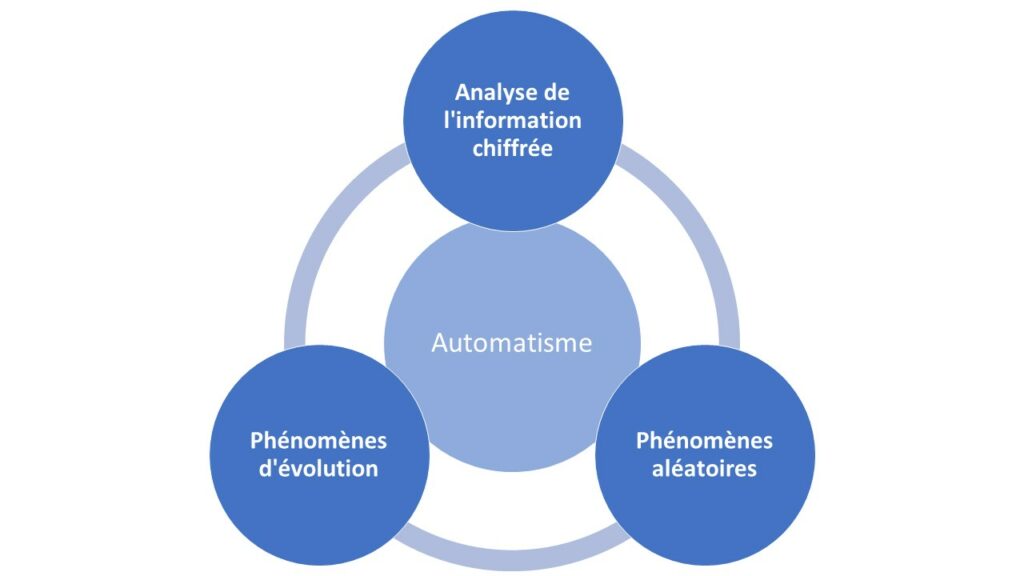
Le programme est structuré autour de trois parties thématiques : 

• analyse de l’information chiffrée (statistiques) ; 
• phénomènes aléatoires (probabilités conditionnelles) ; 
• phénomènes d’évolution (analyse : suites, fonctions, exponentielles, dérivée) ; 

et d’une partie transversale : 

• automatismes (lecture et production de graphiques, traitement de données, calcul numérique et algébrique). 

Les trois parties thématiques présentent les « Contenus mathématiques » en regard des « Situations et problèmes » étudiés. 

Tout d’abord, avec cet enseignement en première, l’élève a la possibilité de prendre l’option mathématiques complémentaires en terminale.
Ainsi il peut choisir une orientation pour des études supérieures ayant une composante mathématique.

Chacune de ces parties fait l’objet d’un article dédié.

Avant de regarder ces aspects techniques nous allons répondre aux questions fondamentales suivantes : 

• Quelles sont les intentions de ce programme ?
• Quelles attitudes cherchons-nous à développer chez l’élève ?
• Quelles sont les compétences mathématiques mises en œuvre et développées ?
• En pratique, comment développer ces aptitudes, compétences et connaissances ?
• En quoi la pensée algorithmique et les outils numériques aident ils à réconcilier l’élève dans son apprentissage ?
• Quelle est l’utilité du cours et de sa trace écrite ?

Quelles sont les intentions de ce programme ?

Quelles sont les intentions de ce programme de mathématiques du tronc commun de Première ?

Que l’élève possède une culture mathématique qui lui permette d’avoir une vie sociale épanouie, une vie citoyenne éclairée et une vie professionnelle réussie.

Qu’il se réconcilie avec les mathématiques, en les mettant en pratique dans un contexte actuel et en observant leur efficacité à traiter des problèmes concrets.

Permettre à l’élève de développer ses aptitudes au raisonnement, à la rigueur, à l’esprit critique, à l’inventivité et à la créativité.

Lui donner des outils et le langage pour comprendre et réfléchir aux phénomènes présents tant dans les différentes disciplines de son parcours d’études, que dans les débats de sociétés actuels.

Quelles attitudes cherchons-nous à développer chez l’élève ?

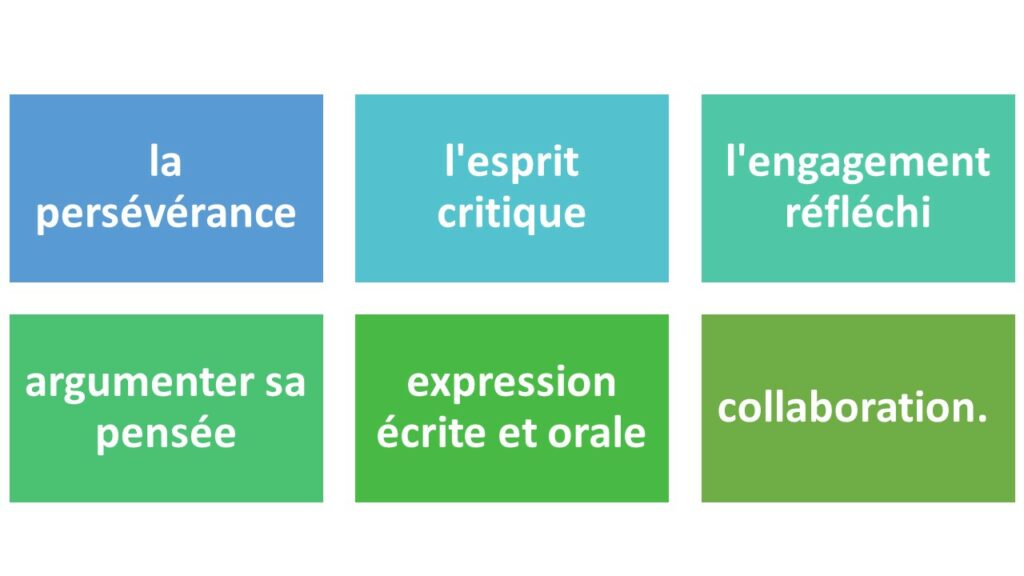
Quelles sont les attitudes que l’élève va développer durant cet apprentissage ? 

• la persévérance dans la recherche d’une solution, 
• l’esprit critique, 
• l’engagement réfléchi dans un débat, 
• le souci d’argumenter sa pensée par un raisonnement logique, 
• la qualité d’expression écrite et orale, 
• l’esprit de collaboration dans un travail d’équipe. 

Quels sont les moyens utilisés pour aider l’élève à les développer : la résolution d’exercices et de problèmes soit individuellement soit en groupe.

Les mathématiques sont là pour répondre aux besoins et questionnements des hommes !

Afin de prendre conscience que les mathématiques sont là pour répondre aux besoins et questionnements des hommes, que c’est une matière vivante et en perpétuelle évolution. Ce qui peut être montré dans un cadre historique et dans la société actuelle 

Quelles sont les compétences mathématiques mises en œuvre et développées ?

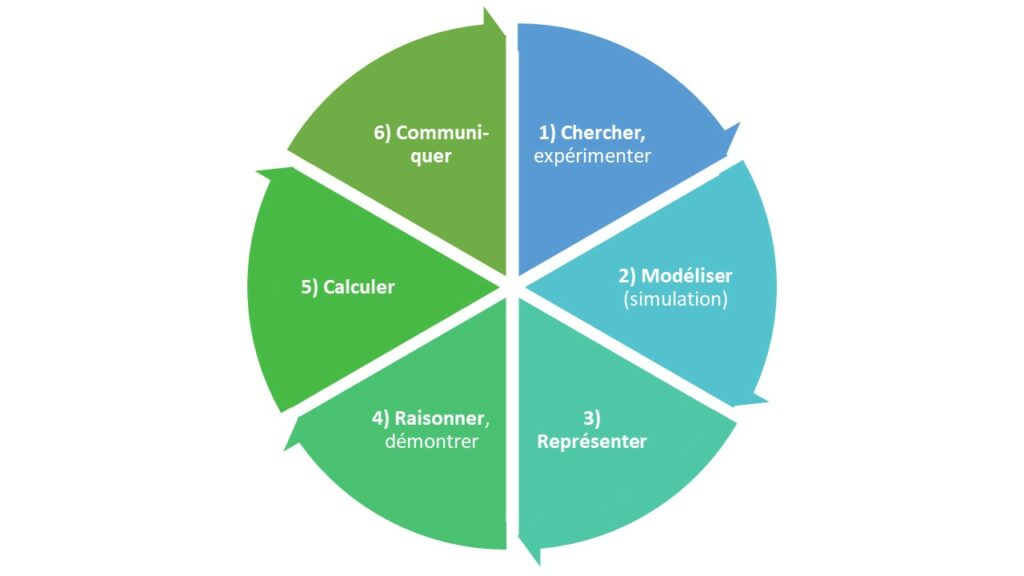
Ceux sont 6 compétences essentielles que l’élève a rencontrées depuis ses premiers pas en mathématiques et pour les années suivantes. 

Ces compétences sont des piliers non seulement pour les mathématiques mais aussi pour les sciences de la nature, les technologies, l’ingénierie et les sciences humaines et sociales.

• chercher, expérimenter, en particulier à l’aide d’outils logiciels ; 
• modéliser, faire une simulation, valider ou invalider un modèle ; 
• représenter, choisir un cadre (numérique, algébrique, géométrique), changer de registre ; 
• raisonner, démontrer, trouver des résultats partiels et les mettre en perspective ;
• calculer, appliquer des techniques et mettre en œuvre des algorithmes ; 
• communiquer un résultat par oral ou par écrit, expliquer une démarche. 

En pratique, comment développer ces aptitudes, compétences et connaissances ?

Par la pratique, c’est-à-dire la résolution de problèmes. Ces problèmes sont en lien avec les autres disciplines, la vie courante ou citoyenne.

Cette pratique repose sur la démarche progressive : manipuler – verbaliser – abstraire.

L’objectif est d’appréhender progressivement les objets mathématiques (un nombre, une fonction, une expérience de probabilité…) sous une forme d’abord concrète, ensuite plus conceptuelle (dessinée ou verbalisée) et enfin s’en construire une abstraction. 

Un des moyens de résolution d’un problème est la modélisation. L’élève conçoit un modèle adapté à la situation étudiée. Il développe son inventivité et sa créativité en imaginant le modèle. Il développe sa rigueur en identifiant les hypothèses qu’il choisit lors de la mise en place de cette modélisation.

En quoi la pensée algorithmique et les outils numériques aident-ils à réconcilier l’élève dans son apprentissage ?

L’algorithmique et les raisonnements mathématiques ont de nombreux points communs : la résolution de problème, l’enchaînement d’opérations, la rigueur. L’élève peut ainsi développer ces compétences en pratiquant ces deux disciplines. 

La mise en œuvre des outils numériques et de la programmation rend ces apprentissages plus dynamiques et interactifs.

L’élève peut visualiser plus facilement l’évolution d’un phénomène via l’exécution d’un programme ou l’usage d’un tableur. Il peut étudier plusieurs modélisations de son problème.

Quelle est l’utilité du cours et de sa trace écrite ?

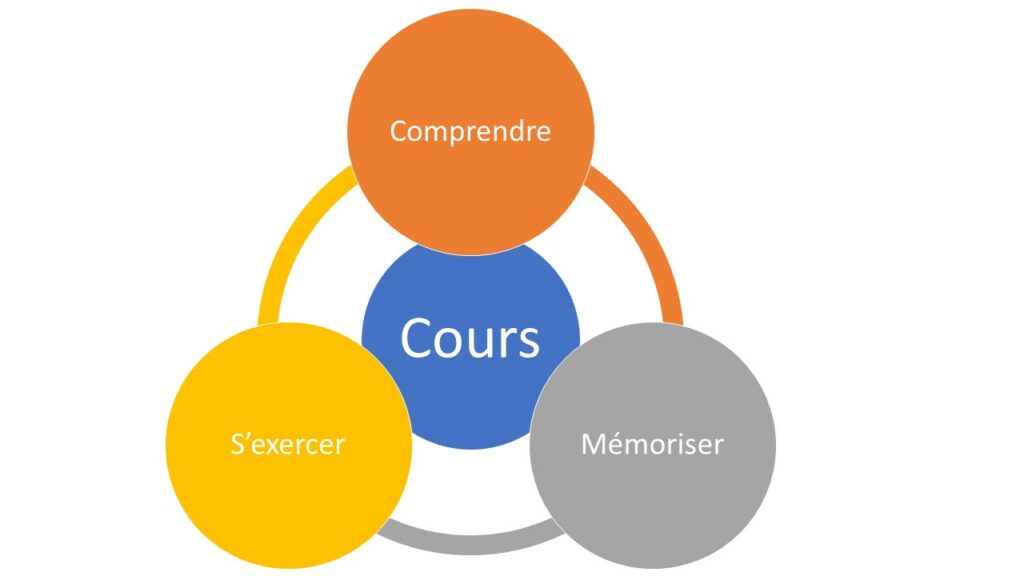
Pour l’élève, la trace écrite récapitule de façon organisée les connaissances, les méthodes et les stratégies étudiées en classe. Elle lui permet de voir et de comprendre les liens entre les différentes notions. Il comprend la nature des différents énoncés : définition, propriété, démonstration, mise en application.

Sa consultation favorise le cercle vertueux Compréhension ⇔ Mémorisation 

Voilà, sans parler maths, les enjeux du programme de maths de première !

Ces enjeux pour les mathématiques sont assez proches d’une classe à l’autre. 

Mais le paradoxe est que bien qu’ils soient fondamentaux et pourtant c’est souvent d’eux dont on parle le moins. Et les aspects techniques parfois rebutants ceux dont on parle le plus !

Voilà pourquoi pour moi il était important de remettre chaque chose à sa place.

Dans nos prochains articles nous allons aborder la description technique du programme.