Voilà plus d’une semaine maintenant que nous sommes confinés pour limiter, pour ralentir, la propagation du Covid-19, afin de ne pas encombrer les hôpitaux. Comme beaucoup j’imagine, je n’en reviens toujours pas.
J’ai l’impression d’être dans un film à grand spectacle, un grand film hollywoodien, où les hommes sont attaqués par un ennemi redoutable et invisible. J’attends encore de rencontrer Bruce Willis ou Tom Cruise qui vont venir sauver le monde… En même temps, vu qu’on ne peut pas sortir, ça ne va pas être facile de les rencontrer !
Nous verrons justement dans une série d’articles quels sont les états par lesquels on passe pendant une crise, afin de mieux la traverser. C’est le moment d’être stoïque, et de bien distinguer ce qui nous appartient, et ce qui ne nous appartient pas, et de ne pas lutter inutilement contre les choses que nous ne pouvons pas changer.
Nous verrons également comment les maths servent pour anticiper, imaginer les scénarios possibles et aider à prendre les décisions pour lutter contre la maladie. Mais aussi comment ce qui nous arrive peut nous permettre de comprendre certaines notions mathématiques.
Les maths pour comprendre la diffusion de la maladie, et réciproquement
Voilà une situation, celle de la pandémie du Covid-19, où les mathématiques sont un outil incontournable. En effet, comment se faire une idée de la propagation du virus dans la population, et choisir des mesures adaptées pour ralentir ou stopper cette propagation?
On peut comprendre que plus il y a de gens infectés (et qui sont ensuite guéries ou malheureusement mortes), plus le virus va s’affaiblir. Car en effet, pour survivre, il a besoin d’infecter des personnes saines. Un virus ne peut pas se reproduire (contrairement à une bactérie), il ne peut que se répliquer, et pour cela il a besoin d’un organisme « hôte », les humains dans le cas du Covid-19.
Le nombre de personnes que peut infecter une personne malade va dépendre de la contagiosité du virus (p), de la durée de la maladie (D), et du nombre de contacts (C) qu’elle va avoir par jour. Ce nombre s’appelle le R0. En première approche, on peut le considérer égal à p×D×C.
Pour le déterminer, on utilise des calculs statistiques ou des méthodes mathématiques. Bien entendu on obtient une estimation, qui varie en fonction des méthodes de calcul appliquées ainsi que des mesures sanitaires prises. On peut dire qu’il dépend du temps (et du lieu). Actuellement, d’après Wikipedia il se situe entre 1,5 et 6,68, suivant les régions du monde.
Le problème c’est quand ce nombre est plus grand que 1. Pour modifier le R0, nous pouvons intervenir sur la variable C, le nombre de contacts qu’une personne infectée a par jour. Vous trouverez dans cet article extrait du blog de David Louapre (chercheur en physique et grand vulgarisateur de sciences) des détails et une simulation possible de l’effet de la réduction de C sur la propagation de la maladie.
Pour réduire ce nombre C, on a la possibilité de mettre en quarantaine les personnes infectées, en effectuant des dépistages massifs (ce qu’ils ont fait en Corée du Sud) ou bien confiner la population (ce qu’on fait actuellement en France et dans la plupart des pays).
Evidemment le nombre de personnes saines et non infectées intervient aussi dans le calcul. S’il n’y a pratiquement plus de personnes saines (non infectées), le virus disparaît.
C’est le principe du vaccin. C’était le parti pris de Boris Johnson en Angleterre, jouer sur « l’immunité collective »: laisser le virus circuler librement, infecter les personnes qui seraient devenues immunisées (ou mortes… naturellement ce dernier point a provoqué un tollé dans la population et finalement il a abandonné cette idée). Néanmoins, c’est une méthode efficace d’un point de vue épidémiologique, car faute de personnes à infecter, le virus se serait naturellement éteint. Une autre source de renseignements intéressante sur l’évolution de la maladie: le blog du docteur Zagury.
On parle beaucoup en ce moment de croissance exponentielle. De quoi s’agit-il? Pour prendre un exemple plus sympa que le Covid-19, intéressons-nous au mythe concernant l’inventeur du jeu d’échec.
Il s’agirait d’un brahmane nommé Sissa, qui aurait proposé ce jeu au roi Shiram, roi légendaire des Indes, qui s’ennuyait. Totalement séduit, ce roi a demandé à Sissa ce qu’il souhaitait en récompense de ce jeu extraordinaire.

Sissa a répondu: « je souhaite que vous déposiez un grain de riz sur la première case, deux sur la deuxième, quatre sur la troisième et ainsi de suite en doublant à chaque fois ce qu’il y a dans la case précédente, jusqu’à remplir l’échiquier » (qui compte 64 cases). Selon la légende, le roi s’est mis en fureur, considérant que la demande de Sissa était beaucoup trop modeste et qu’en conséquence il se moquait de lui. Le pauvre Sissa a failli y laisser sa vie.
Le vizir du roi, qui était aussi son grand argentier, s’est mis également en fureur, mais pour une autre raison, car lui, savait compter: En effet le nombre de grains de riz serait égal à 1+2+2²+2³…+263 , soit 264-1 , ce qui fait exactement 18 446 744 073 709 551 615 grains, ce qui correspond à 1000 fois la production de riz en 2012. Source Wikipedia et ma mémoire).
Ce qu’il faut comprendre
Une quantité croit de manière exponentielle si à chaque étape on la multiplie par un même nombre, plus grand que 1. Si on la multiplie par un même nombre plus petit que 1, elle décroit vers 0 de manière exponentielle aussi.
Si on part de 1, et qu’on ajoute 2 chaque jour, il faut 50000 jours pour dépasser 100000.
Si on part de 1 et qu’on multiplie par 2 la quantité chaque jour, il faut 17 jours pour dépasser 100000. Voilà la croissance exponentielle.
Mais dans le cas de la propagation d’un virus, c’est beaucoup plus compliqué que cela. On ne multiplie pas le nombre de malades par 2 chaque jour, il y a aussi ceux qui guérissent, et le taux de propagation qui évolue.
Une phrase en tendue dans les médias » En Chine, on note une diminution de l’augmentation des cas« . Cela me rappelle la célèbre phrase concernant « l’inversion de la courbe du chômage ». En ce moment, j’imagine que chacun serait d’accord avec l’idée qu’on aimerait « inverser la courbe d’infection au Coronavirus« .
Mathématiquement, qu’est-ce que cette phrase veut dire ?
Il s’agit de la vitesse de propagation. La vitesse de propagation peut augmenter de jour en jour, c’est la première partie de la courbe, puis attendre un pic (c’est au niveau du point d’inflexion), et ensuite diminuer. Donc attention, on constate toujours une augmentation du nombre de cas, mais moins forte. Sur la courbe, on constate que sur la première partie, « le creux de la courbe » est tourné vers le haut, sur la deuxième partie, « le creux de la courbe » est tourné vers le bas. Les lycéens de Terminale connaissent bien cette notion: il s’agit de la convexité.
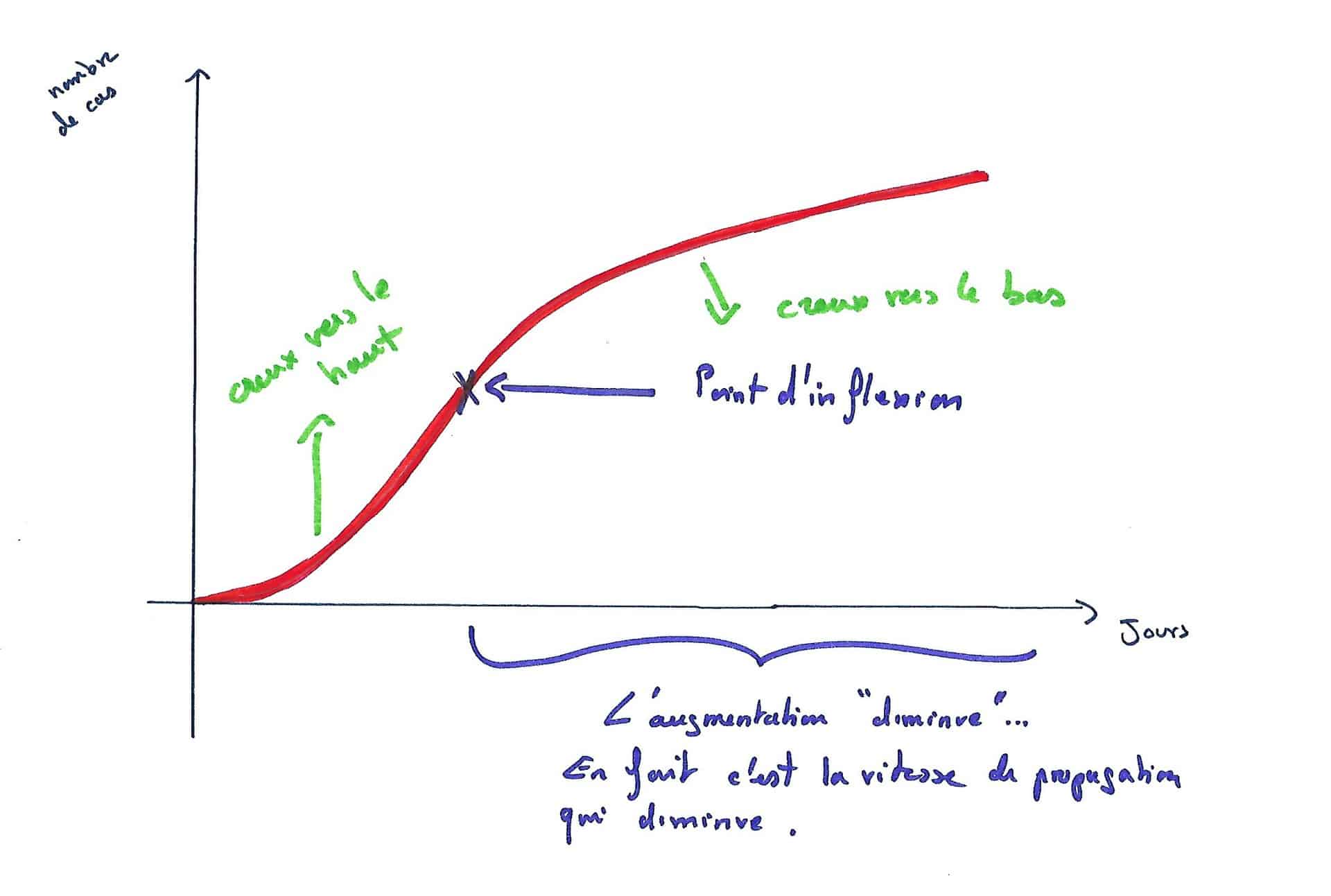
Donc une diminution de l’augmentation est-ce une bonne nouvelle ?
Je vous laisse juge.