Mathématiques et créativité

Introduction

Mathématiques et créativité, ce sont deux mots que l’on n’associe pas spontanément. Pourtant, si on regarde le chemin parcouru depuis le temps où nos ancêtres comptaient leurs moutons avec des cailloux (d’où l’origine du mot calcul au passage : calculus = caillou en latin. La légende prétend que les bergers comptaient leurs moutons à l’entrée et à la sortie d’un enclos, en utilisant un pot rempli de cailloux. Un caillou dans le pot pour chaque mouton qui entre, et ensuite un caillou sorti du pot pour chaque mouton qui sort. Ils avaient déjà découvert le principe de la bijection… Mais c’est une autre histoire), le moins qu’on puisse dire, c’est qu’on en a créé des objets mathématiques ! (Certains disent qu’on les a simplement découverts… voir cet article )

Dans cet article, écrit avec Emmanuel Amiot , nous allons vous raconter quelques inventions mathématiques.

Les maths : résolution de problèmes, avec des outils existants…ou inventés

Les maths, qu’est-ce que c’est ? Il y a pas mal de réponses possibles. Voici mes préférées :

• C’est une méthode de résolution de problèmes
• C’est un questionnement permanent
• C’est un jeu
• C’est une recherche de la vérité
• C’est un monde, et même plusieurs
• C’est un langage ; c’est le langage dans lequel est écrit le monde qui nous entoure
• C’est une manière de raisonner

Et vous, quelle est votre réponse ?

Si on regarde les maths en tant que méthode de résolution de problèmes, voici le procédé :

• On identifie le problème : par exemple combien faut-il ajouter à 5 pour obtenir 8 ?
• On cherche dans sa boîte à outils : ici on va chercher dans les tables d’addition, ou on compte sur ses doigts, ou sur un boulier, ou avec des cailloux…
• On trouve, ou on construit la réponse : 3.

Que se passe-t-il si on ne trouve rien dans sa boîte à outils ? C’est là le génie (ou le caractère « gonflé ») des mathématiciens : on invente des outils, ou des objets.

Au passage, on invente aussi un langage commode pour exprimer les problèmes. Ce langage nous permet alors de se poser de nouvelles questions.

Le problème exposé ici se note : Résoudre l’équation 5+x=8.

Dès lors, on peut considérer le problème : Résoudre l’équation 7+x =3 . (C’est déjà un acte créatif. Transformer les données.)

Seulement, là, à l’époque lointaine (avant le 2^ème siècle avant JC) où les nombres négatifs n’avaient pas été inventés, ce problème n’avait pas de solution.

Les nombres négatifs

On peut considérer qu’on a inventé les nombres négatifs pour pouvoir résoudre l’équation a+x = b, pour toutes les valeurs entières prises par a et b. On savait le faire quand a était un nombre « entier naturel » plus petit que b, mais sinon non. Les mathématiciens ont donc inventé des nouveaux nombres, les nombres qu’on a appelés bien plus tard « négatifs », afin d’avoir des solutions à cette équation.

Il est amusant de constater que le mot « positif » en français a été utilisé avant le mot « positif » en maths (1751, encyclopédie) ; positif veut dire : certain, réel, posé et cela s’oppose au départ à naturel, par exemple dans « la loi positive » (créée par l’homme), par opposition à la loi « naturelle » (de la nature), alors qu’en maths un entier « naturel » est « positif » !

Introduction aux nombres négatifs (attention, blague de matheux…)

Un homme et une femme rentrent dans une pièce absolument vide. Un certain temps après, trois personnes ressortent. Que s’est-il passé ?

• « Bah, c’est la nature », répond le biologiste
• « Mais non, c’est une erreur de mesure » rétorque le physicien.

Le mathématicien quant à lui, après avoir longuement réfléchi, comme tout mathématicien qui se respecte, dit : « si maintenant une personne rentre dans la pièce, alors elle sera vide ».

Note pour le lecteur : vu que 2=3+(-1), il y a « -1 personne dans la pièce » quand les 3 personnes en ressortent. Or 1+(-1)=0.

Les nombres « négatifs » se définissent « en miroir » des nombres naturels (les nombres naturels que l’on qualifie désormais de positifs). L’existence ou la réalité des nombres négatifs, même si elle va plutôt de soi maintenant, a mis longtemps à s’établir. Autant elle est assez compréhensible dans le monde marchand, avec les systèmes de recettes et de dépenses, autant dans le monde mathématique elle est restée longtemps problématique. Quand Diophante (IIIème siècle) trouve une solution négative à une équation, il la traite « d’absurde ».

En Occident il en sera de même jusqu’au XVIIème siècle environ. Les solutions négatives d’équations ne sont pas considérées comme des solutions. On les traite de « feintes », « d’absurdes » ou « fausses », ou on les réinterprète comme des solutions positives.

(Une anecdote amusante : une de mes élèves m’a dit que l’équation 2x=0 n’avait pas de solution. En effet, pour elle, 0 ne pouvait pas être une solution, parce que 0 c’est rien !)

Parler d’un nombre « plus petit de zéro », ou « moins que rien », c’est assez difficile à concevoir, car 0 est considéré, encore de nos jours, comme le « plus petit des nombres ». Il faudrait sans doute distinguer ici « grandeur » et « nombre ».

Bref, ce sujet passionnant a donné l’occasion de nombreux débats, que nous ne reprendrons pas ici.

Retenons que les nombres négatifs ont été « inventés », et que somme toute, ils sont bien pratiques.

Au passage il est établi par les neuropsychologues (en particulier Stanislas Dehaene; pour en savoir plus) que les nombres préexistent dans le cerveau humain, mais il parle des nombres positifs. Cela n’a pas l’air d’être le cas pour les nombres négatifs.

Le problème rencontré par les élèves du XXIème siècle, une fois accepté l’idée de l’existence des nombres négatifs, est la difficulté de notation. En effet, le symbole « – » désigne trois choses différentes :

• « -3 », un nombre négatif
• « 5 – 2 » , une opération entre deux nombres
• « – x » , l’opposé de x. À ce dernier titre, « – x » peut désigner une quantité positive.

Pourtant, même de brillants étudiants de classes préparatoires associent le symbole « – »   à « négatif  » !

Quel est le signe de 0 ? Il est également amusant de remarquer que pour les français, le nombre « 0 » est le seul à être à la fois positif et négatif, alors que pour les anglo-saxons, il est « non  positif » et « non négatif ». (C’est dû à la différence entre inégalités strictes ou larges).

Dans ce nouvel ensemble, contenant les entiers positifs, 0 et les entiers négatifs, non seulement les équations a+x=b où a et b sont des entiers positifs ont toutes des solutions, mais également les équations a+x=b où a et b peuvent être des entiers négatifs aussi ! Il a fallu un peu « mouiller la chemise » pour étendre les opérations (+, -, x, ÷) à ce nouvel ensemble, mais le gain final est vraiment significatif. Ce nouvel ensemble s’appelle l’ensemble des entiers relatifs.

Les fractions

Voilà aussi une notion bien délicate. Que se représentent les élèves ou même certains adultes quand on leur parle de  3/7? Souvent pas grand-chose.

Pourquoi les fractions ont-elles été inventées ? Pour résoudre les équations du type « 7x=3« . On peut remarquer que l’équation «2x=6 » admet une solution entière (3), mais pas « 7x=3« . On peut partager certaines quantités, mais pas toutes.

Une fraction, comme son nom l’indique, sert à « fractionner ». Or certaines choses sont difficiles à imaginer « fractionnées ».

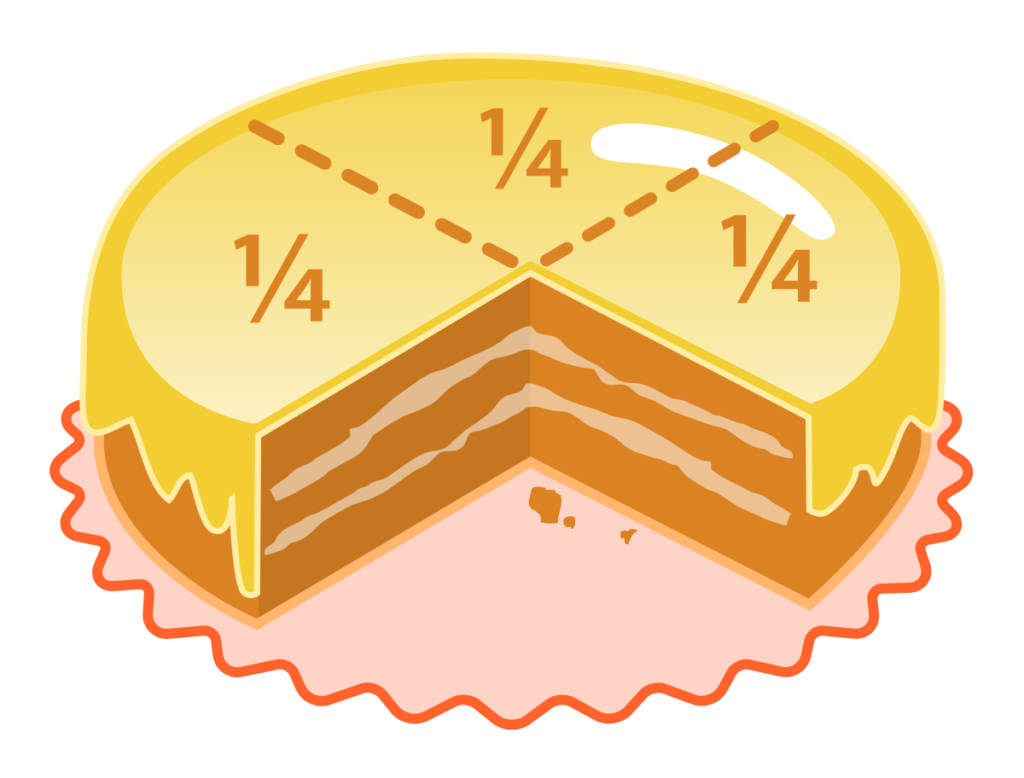
Voici un conte ancien :

Dans un lointain pays, à une lointaine époque, vivait un homme qui avait trois fils et un troupeau de chameaux. A sa mort, il exprima sa dernière volonté : « mes chers fils, voici comment vous allez vous partager le troupeau : l’aîné en aura la moitié, le cadet le tiers et le dernier le neuvième ». Une fois leurs chagrin passé, les fils s’attelèrent au partage du troupeau. Or celui -ci était constitué de 17 chameaux…

On comprend tout de suite la difficulté, car bien entendu il ne s’agissait pas de couper des chameaux ! les trois fils se lamentaient, ils ne pourraient pas suivre les dernières volontés de leur père (et en ce temps-là, c’était sacré les dernières volontés d’un mort…)

Un voisin les prit en pitié et leur donna un de ses chameaux. Le troupeau contenait alors 18 chameaux. L’aîné en pris donc 9, le cadet 6 et le benjamin 2. Il en resta donc un, qu’ils purent rendre au voisin. Tout le monde a été ravi !

Les fractions ont donc été inventées pour que l’on puisse imaginer toutes les divisions possibles de deux nombres entiers, autrement dit pour que les équations du type « ax=b » aient toujours une solution (sauf si a=0). Au départ on s’est proposé de la noter « a/b« .   Mais cela a été un peu plus compliqué que dans le cas des nombres négatifs, puisque on s’est rendu compte qu’une même « grandeur » pouvait avoir plusieurs écritures. Par exemple « 1/2=2/4=4/8« 

Bref, après du travail, les mathématiciens ont construit un nouvel ensemble de nombres, les nombres rationnels, qui contient tous les entiers (positifs et négatifs) et toutes les solutions des équations « ax=b« , où a et b sont deux nombres entiers (relatifs), avec a non nul. Et cerise sur le gâteau, dans cet ensemble, toutes les équations « ax=b » où, cette fois a et b sont des nombres rationnels quelconques (avec a non nul) ont également toutes des solutions ! Et on a conservé la possibilité de résoudre également les équations du type « a+x=b« , avec a et b nombres rationnels. Ce qui fait que dans l’ensemble des nombres rationnels, on peut résoudre toutes les équations dites du « premier degré », du type « ax+b=0« , avec a et b rationnels et a non nul.

Les nombres réels

On ne s’est pas arrêté en si bon chemin. Dans l’ensemble des nombres rationnels, toutes les équations du premier degré ont bien une solution. Mais qu’en est-il des équations du second degré ? Par exemple x²=2 ? On démontre en classe de seconde (par l’absurde) qu’il est impossible de trouver une solution dans l’ensemble des nombres rationnels.  ( A tout seigneur tout honneur, c’est Euclide qui a proposé une première démonstration de ce résultat.)

Pour pouvoir introduire les racines carrées de tous les nombres positifs et pour d’autres raisons, on a créé les nombres réels.

Jusque-là, même si la définition mathématique des nombres réels est délicate, tout se passe à peu près bien. On reste dans la réalité. Même si les nombres qu’on a dû « rajouter » s’appellent des nombres irrationnels… Un comble pour les mathématiques ! Et dire qu’on reproche souvent aux mathématiciens d’être « trop rationnels » et de manquer de fantaisie… C’est bien mal les connaître !

Les nombres réels contiennent donc tous les nombres rationnels et donc bien d’autres nombres. Et chose remarquable, les nombres « irrationnels » sont bien plus nombreux que les nombres rationnels. (Même s’il y en a un nombre infini. Alors il y a plusieurs sortes d’infinis? Et oui! Il y a même une infinité de sortes d’infinis. Une première approche dans cet article.)

Les nombres complexes

Dans l’ensemble des nombres réels, toutes les équations du type x²=a, avec a un nombre réel positif ont des solutions (deux exactement si a est non nul). Mais quid de l’équation x²=-1 ? Alors là quand même c’est exagéré ! On nous bassine depuis le collège qu’un « carré est toujours positif » ! C’est quoi cette trahison ? (J’ai rencontré plusieurs adultes qui avaient un souvenir cuisant de leur rencontre avec les nombres complexes. Ils se sentaient littéralement trahis…)

Les mathématiciens qui ont osé imaginer une telle « monstruosité » (un « nombre » dont le carré vaut -1) étaient dans leurs petits souliers. Ce sont Cardan et Bombelli qui ont commencé à l’utiliser au XVIème siècle. En effet c’était bien pratique pour résoudre les équations du troisième degré.

Considérons l’équation x³-15x+4=0. Elle admet 4 comme solution. Cardan avait mis au point une méthode pour résoudre ce type d’équation (x³+px+q=0), qui nécessitait de calculer, entre autres, des racines carrées. Ça se passait bien quand les nombres étaient positifs. Mais sinon…

Attention, un peu de maths dans ce qui suit :

Mais les nombres complexes étaient nés. C’est Gauss qui les a baptisés « nombres complexes » en 1831.

Sans le savoir Gauss a mis dans l’embarras les professeurs de mathématiques : en effet « complexe » n’est pas très engageant. Quand on dit aux élèves de terminale qu’on va étudier les nombres complexes, ils s’attendent à quelque chose de difficile. Et de fait ils le trouvent difficile. S’il les avait appelés autrement, (nombres extraordinaires, nombres charmants, etc.) la face de l’enseignement aurait été changée.

De même qu’il a été d’un grand secours d’associer les nombres réels à une droite, cela a permis de les représenter, les visualiser, il a été extrêmement fertile d’associer un nombre complexe a un point du plan.

En effet, un nombre complexe se définit par deux nombres réels, et un point du plan également. A partir de cette simple constatation, on a pu faire de la géométrie avec des nombres complexes, et ça c’est quand même assez fort.

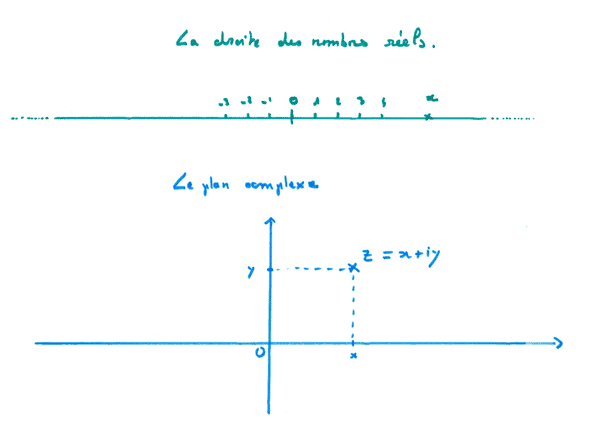
Il est une dernière chose remarquable, c’est que finalement, on a inventé les nombres complexes pour pouvoir résoudre les équations du second degré, et par la suite, on a pu démontrer que dans cet ensemble, toutes les équations polynomiales de n’importe quel degré ont des solutions, et toutes leurs solutions sont dans l’ensemble des nombres complexes. Pas la peine d’inventer un nouvel ensemble pour pouvoir résoudre ces équations. Et ça, ce n’était pas prévu, et c’est vraiment extraordinaire !

Ces deux ensembles (les réels et les complexes) se sont révélés beaucoup plus riches que ce qu’on pouvait imaginer au départ.

Les sommes infinies convergentes

Les paradoxes de Zénon

Zénon d’Elée (5^ème siècle avant JC) est un philosophe grec, célèbre pour ses paradoxes. Il voulait montrer que l’évidence des sens est trompeuse, et que le mouvement est impossible. Ce qui est intéressant avec ses paradoxes, ce sont les différentes façons de les réfuter. Les mathématiques ont apporté une réponse bien plus tard, au XVIIème siècle, avec la notion de limite.

Voici un de ces paradoxes :

C’est le paradoxe de la pierre lancée vers un arbre. Zénon se tient à huit mètres d’un arbre, tenant une pierre. Il lance sa pierre dans la direction de l’arbre. Avant que le caillou puisse atteindre l’arbre, il doit traverser la première moitié des huit mètres. Il faut un certain temps, non nul, à cette pierre pour se déplacer sur cette distance. Ensuite, il lui reste encore quatre mètres à parcourir, dont elle accomplit d’abord la moitié, deux mètres, ce qui lui prend un certain temps. Puis la pierre avance d’un mètre de plus, progresse après d’un demi-mètre et encore d’un quart, et ainsi de suite avec une infinité d’étapes. Zénon en conclut que la pierre ne pourra frapper l’arbre qu’au bout d’un temps infini, c’est-à-dire jamais.

La notion de limite

L’idée qu’a développé l’analyse moderne, c’est qu’une somme infinie de termes positifs peut avoir une valeur finie.

Il faut pour cela introduire la notion de limite. Il ne s’agit pas ici de faire un cours de mathématiques, donc je vais vous donner une idée « intuitive » de la notion de limite, telle qu’elle est introduite au lycée d’ailleurs. Considérons la suite de nombre : 1 ; 1/2 ; 1/4 ; 1/8 ; 1/16 ; …. et ainsi de suite. Si vous utilisez une machine pour les calculer, vous obtenez des nombres de plus en plus petits avec de plus en plus de « 0  »: 1 ; 0,5 ; 0,25, 1,125 ; 0,0625 ;  au bout d’un moment la machine n’affichera plus que « 0 » (car les nombres dans une machine n’ont qu’un nombre limité de décimales) ou une erreur. Avec une machine de collège, on trouve 1/2¹⁰⁰=0,0000……000007888609052, avec 31 « 0 ».

Bref, s’il s’agit d’une quantité de sucre dans un litre d’eau, on pourrait considérer que le sucre a totalement disparu.

Dans le cas du paradoxe de la pierre, voici ce qu’il se passe : (attention, un peu de maths dans ce qui suit)

Un peu de théorie

Les sommes infinies divergentes

Tout est dans -1/12

Nous avons donc vu comment le concept de proximité, de limite, permet de donner un sens à une somme infinie et de résoudre ainsi le paradoxe de Zénon. On utilise aussi le mot « série » pour parler de somme infinie.

Mais que dire de ces séries dont les sommes finies (les sommes partielles) refusent de se stabiliser autour d’une valeur limite ?

Par exemple, la série

1-1+1-1+1-1+1-1++1-1+1-1+1-1+1-1+1-1+1-1+1-1+1-1+1-1+1-1+1-1…

a été discutée depuis le moyen âge (on dit que certains ont été brûlés pour leurs affirmations à son sujet, faites attention). On ajoute alternativement 1 ou -1, ce qui peut faire penser à un clignotant.

Les sommes partielles valent

1

1-1=0

1-1+1=1

1-1+1-1=0 …

et ainsi de suite, alternativement 1 et 0. Or il n’existe aucun nombre qui soit approché de plus en plus près aussi bien par une suite de 0 que par une suite de 1 ! (Sauriez-vous le prouver rigoureusement ?) Cependant, on peut avoir envie de « couper la poire en deux » et de décréter que cette série « donne » la valeur 1/2, « moit-moit » entre les deux valeurs 0 et 1 entre lesquelles elle oscille.

À l’appui de cette affirmation osée, vous verrez souvent sur Internet ou ailleurs le calcul gonflé suivant qui sera central dans la suite :

admettons que cette somme infinie 1+1-1+1-1+1-1+1-1+1-1+1-1+1-1+1-1… ait une valeur, que l’on appellerait S (comme somme, ou alors comme saugrenu). Regardons le calcul simple suivant, où j’écris deux fois S, dont une avec un décalage :

S = 1 -1+1 -1+1-1+1-1+1-1+1-1+1-1+1-1…

S = 0+1 -1+1-1+1-1+1-1+1-1+1-1+1-1+1-1…

Maintenant additionnons terme à terme ces deux lignes. Le premier 1 reste tout seul. Il est le maillon faible. Comptons-le quand même ! Ensuite on a -1 dans la première ligne et 1 dans la seconde. La somme des deux vaut donc 0. Le terme suivant est au contraire 1 additionné à -1 mais le résultat est encore 0. De même pour tous les suivants. On s’est donc ramené à une somme infinie qui ne pose aucun problème, elle :

1+0+0+0+0+… qui vaut clairement 1.

Or c’est le résultat de l’addition de S à elle-même. Donc 2S = 1, soit S = 1/2.

Êtes-vous convaincu par ce calcul ? Ou avez-vous l’impression d’une arnaque ? C’est en fait le cœur de la question posée par cet exposé ! (Indication : oui, c’est une arnaque, mais le résultat est vrai en un sens que nous allons voir).

Revenons à l’hypothèse faite. L’avez-vous observée au passage ? On suppose que S existe, et ce n’est pas rien ! En fait au sens développé dans le paragraphe précédent, S n’existe nullement !!!

Ce que l’on a fait (et c’est intéressant quand même) c’est montrer que si l’on veut absolument associer une valeur à S, en respectant des propriétés de calcul simples et élémentaires, alors S ne peut pas valoir autre chose que 1/2.

Je parle des propriétés de calcul simples et élémentaires car nous en avons utilisé un paquet, mine de rien:

1. Qu’une somme infinie, si elle a une valeur, n’en a pas d’autre !
2. Qu’on ne change pas la somme en décalant la série. Ici on a dit finalement que
   1+1-1+1-1+1-1+1-1+1-1+1-1+1-1+1-1… c’est pareil que 0+1+1-1+1-1+1-1+1-1+1-1+1-1+1-1+1-1…
3. Qu’on peut ajouter terme à terme deux sommes infinies : autrement dit que si
   S = a + b + c +…  et S’ = a’+b’+c’+… alors
   S+S’ = (a+a’) + (b+b’) + (c+c’)…
4. Que notre univers des sommes saugrenues est compatible avec la convergence « officielle » étudiée avant (ici on mélange un S très douteux avec une somme sans ambiguïté, 1+0+0+0+…).

En fait, on peut rendre cela rigoureux en disant qu’on appelle procédé sommatoire toute méthode qui permet d’attribuer à une série une valeur, tout en respectant les propriétés précédentes (et quelques autres pour bien faire dont on fera grâce). Le calcul « arnaque » aura alors constitué une démonstration, en un sens rigoureux, du fait suivant:

Tout « procédé sommatoire » qui attribue une valeur à la somme

 1-1+1-1+1-1+1-1+1-1+1-1+1-1+1-1… trouve pour valeur 1/2.

Avant de pousser un grand soupir de satisfaction, posons-nous la question : existe-t-il de tels procédés sommatoires ?

Mathématiquement, la propriété précédente prouve une unicité. C’est bien, mais cela ne dispense nullement de donner une preuve d’existence! Les deux vont souvent de pair, mais se démontrent de manière tout à fait indépendante.

Il existe des présentations de différents procédés sommatoires. Nous allons nous concentrer sur l’un d’entre eux, qu’il faudra pousser dans ses derniers retranchements pour parvenir à l’étonnant résultat annoncé par le titre !

Avant cela, je voudrais vous entraîner au « tour de magie » sur d’autres séries. Posons pour commencer (donc tout à fait abusivement !)

T = 1-2+3-4+5-6+… et faisons-lui subir le même coup du décalage :

T = 0+1-2+3-4+5-6+…

En additionnant verticalement, on trouve 1+0, -2+1, 3-2… soit

2T = 1-1+1-1+1-1… = S !

Ayant retrouvé S et calculé sa (seule) valeur (possible), on en déduit T=1/4.

Petite complication, au lieu des entiers dans l’ordre et sans exception, prenons les nombres de Fibonacci , que je vous donne en vrac pour que vous ayez le plaisir de trouver vous-même leur logique propre:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …

Cette séquence (étudiée par Léonard de Pise début XIIIe siècle) a des propriétés fascinantes, mais contentons-nous de chercher sa somme.

Comme les précédentes, elle est saugrenue, au sens où les sommes finies ne se stabilisent jamais au contraire, celles-ci augmentent vertigineusement (avez-vous remarqué quelque chose quant à leurs valeurs ?). Néanmoins, si on insiste pour qu’il y ait une valeur, alors celle-ci est unique et nous allons la calculer avec le truc du décalage :

F = 1+1+2+3+5+8+13+21+…

F = 0+1+1+2+3+5+ 8+13+21+…

2F = 1+2+3+5+8+13+21+…

et dans la dernière somme, on reconnaît presque F: il manque le premier « 1 ». C’est donc F -1 (sauf que je n’avais pas mis ça dans les règles des « procédés sommatoires ». Pouvez-vous formuler la règle manquante, qui a l’air aussi évidente que les autres ?).

La fin est triviale : 2F = F – 1, d’où à la stupéfaction générale F = -1 !!!

Nous sommes maintenant prêts à justifier que :

la seule valeur possible pour la somme de tous les entiers 1+2+3+4+… est -1/12.

Appelons en effet M cette somme mystérieuse : M = 1 + 2 + 3 + 4 + 5 + …

Vous trouverez facilement sur le Net ou dans des TeD-talks le calcul suivant, qui fait appel à toutes les ressources que nous avons déjà mobilisées (mais nous irons plus loin) : on va utiliser et le décalage et les résultats des calculs précédents !

Voyez :

M = 1 + 2 +  3 + 4 + 5 + 6 +…

–T = -1+ 2 –  3 + 4 –  5 + 6 +…

M-T=0 + 4 + 0 + 8 + 0 + 12 + … = 4 ( 1 + 2 + 3 + …) = 4 M.

L’équation 4M=M-T fournit rapidement 3M=-T , d’où M= -T/3=-1/12 !

Au passage j’ai utilisé implicitement des règles de calcul qui gagneraient à être explicitées (factoriser le 4, jeter les 0…)

Tout ceci a-t-il un sens ?

Comme discuté plus haut, ces calculs montrent une propriété d’unicité : SI il existe une façon de calculer ces sommes, alors la valeur ne peut être que celle proposée. Mais existe-t-il de tels « procédés sommatoires » ?

Fonction génératrice et procédé sommatoire d’Abel

Une méthode féconde et encore presque compréhensible est la suivante : étant donné une séquence (commençons par le « clignotant, 1+1-1+1-1+1-1+…), on multiplie chaque terme par une puissance croissante d’une inconnue x. Cela donne dans ce cas

Or on peut calculer cette somme, ici en reconnaissant l’expression d’une série géométrique :

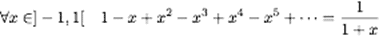
Ce que nous voulons est donner un sens à cette somme infinie quand x=1 (notez que cela est exclu dans l’identité ci-dessus !). Or de nouveau l’opération de passage à la limite permet de fournir une réponse : en effet,

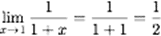
Le graphique ci-dessous illustre que l’on peut effectivement « aller jusqu’à x=1 », de façon « lisse » (on pourrait même aller au-delà).

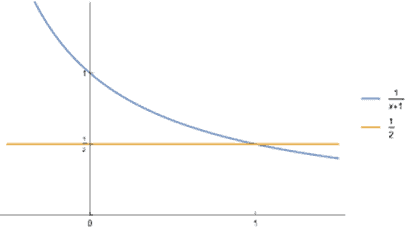
Le même procédé fonctionne pour la somme T : en effet, on démontre assez facilement que,

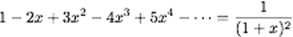
La preuve mérite un détour : essayez de multiplier la somme de gauche par 1+x, deux fois de suite (multipliez par 1, multipliez par x et ajoutez les deux résultats), à la fin tout se simplifie et il reste 1.

Encore une fois ce résultat ne fait sens que si -1< x <1, mais en passant à la limite on arrive au résultat déjà trouvé !

Notez bien que ce procédé ne fonctionne pas toujours : ainsi

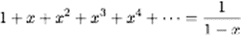
n’a pas de limite quand x tend vers 1, quel que soit le procédé essayé !

On rencontre un problème plus subtil pour la série de Fibonacci, et celui-là va avoir une solution. En effet,

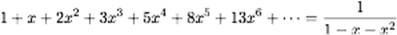
Ceci mérite quelques précisions. On va vérifier tout d’abord que

En effet, en utilisant la distributivité de la multiplication il vient

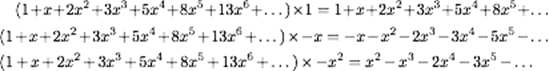
et en additionnant on trouve juste 1, à cause des relations 1+1=2, 2+1=3, 3+2=5 etc., qui sont précisément celles qui définissent la suite de Fibonacci (on rend ce calcul rigoureux par un raisonnement par récurrence).

Un problème plus subtil et presque fatal est la question de la validité de cette relation : quand est-ce que

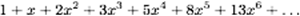
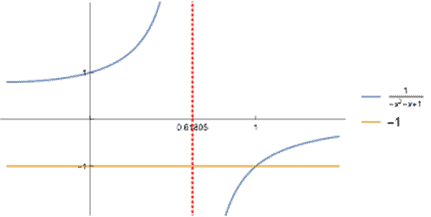
a un sens non saugrenu? Ce n’est pas une série géométrique et la réponse demande un peu de connaissances (par exemple, la règle de d’Alembert, pour les amatrices). Et elle est frustrante :

cette série ne converge que pour |x|<0.61805…

(la valeur exacte est )

On a donc un trou infranchissable pour rejoindre la valeur x = 1 tant désirée !

On peut certes poser x = 1, mais qu’est-ce qui assure la liaison avec la formule qu’on a laissée à gauche de la valeur critique 0.618… ?

Allons dans l’ensemble des nombres complexes : Prolongement analytique

La solution est d’une simplicité et d’une élégance rare : nous allons utiliser une autre extension des mathématiques, celle aux nombres imaginaires !

En effet, l’expression qui ne « passe pas » de 0 à 1 par les nombres réels est parfaitement définie quand x devient un nombre imaginaire, ce qui va permettre de contourner le problème. Voici un graphe de la même fonction, mais avec x complexe. En noir, le graphe d’un chemin qui relie x=0 à x=1, mais en passant par les nombres complexes.

Ce graphe représente l’image complexe d’un nombre complexe grâce au jeu des couleurs : la hauteur d’un point représente le module (la longueur) du nombre complexe image, et la couleur son argument (sa phase). Si vous ne connaissez pas ces notions, croyez-moi sur parole en tout cas ce que l’on voit bien sur le dessin : on peut aller sans problème en x= 1, en contournant le big problème en x = 0.618… !

On peut donc appliquer la méthode de passage à la limite en faisant tendre x vers 1, quitte à passer parfois par les nombres complexes.

Mais en quoi cela permet-il de donner un sens à la somme 1+2+3+4+… ? La méthode que nous venons d’exposer échoue lamentablement, en effet

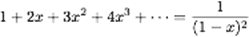
et quoi qu’on fasse, que x, soit réel, imaginaire, ou parfumé à la fraise, quand il s’approche de 1 tout explose ! La solution passe par une autre fonction magique et encore assez mystérieuse, la fonction zêta de Riemann.

Fonction zêta de Riemann

Cette fonction très célèbre mais difficile est définie par :

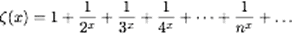
(au moins vous aurez appris la lettre zêta, ancêtre grec de notre « Z »…)

Au départ (sous la plume de Léonard Euler par exemple), ceci n’a de sens que pour x>1. En particulier elle explose pour x = 1 (on trouve la fameuse série harmonique).
Mais progressivement on s’est aperçu que le domaine de validité de cette fonction pouvait s’étendre, d’abord aux nombres complexes de partie réelle >1, puis en fait à tous les nombres complexes — et qu’on pouvait trouver ses valeurs facilement à partir des valeurs « faciles » quand Re(x)>1.  Le graphe en couleur en fait foi :

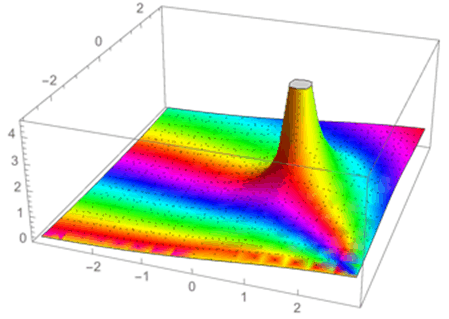
La fonction se prolonge à tous les nombres complexes (sauf 1).

En particulier, on a ce qui ne saurait vous surprendre à ce stade !

Conclusion

Ces différents exemples permettent, nous l’espérons, de voir l’immense créativité des mathématiciens. On remarque aussi qu’on créé des nouveaux espaces pour résoudre des problèmes. Même si ce sont des problèmes qui ne semblent pas avoir de lien avec « la réalité », comme les nombres complexes, il se trouve qu’une fois les nouveaux « objets » créés, ils ouvrent un champ nouveau. Nouveau vocabulaire permettant de modéliser des phénomènes physiques, biologiques ou économiques. Par exemple l’introduction des nombres complexes a permis d’exprimer simplement les phénomènes électriques ou ondulatoires, ce qui permet ensuite de mieux comprendre et de progresser.

Votre électricien n’a aucun scrupule à utiliser les nombres imaginaires, comme vous l’aurez compris en lisant sa facture !