
Comment et pourquoi les apprendre ?
Les tables de multiplication, c’est un problème pour beaucoup d’entre nous . Les apprendre, les faire apprendre à nos enfants, à nos élèves ….
Cet article reprend les idées que j’ai développées dans mon e-conférence du 18 avril 2021, que vous pourrez retrouver dans la vidéothèque.
Trucs et astuces pour mémoriser les tables
Tout d’abord, il faut comprendre le fonctionnement de la mémoire :
- La mémoire est associative
- La mémoire est reconstructive
- La mémoire est répétitive
- La mémoire oublie ce qui ne sert pas
Ce qui veut dire que pour bien mémoriser, c’est important de faire des associations, que l’on mémorise quand on se teste, qu’il faut le faire souvent et qu’il faut s’en servir. Ce n’est pas en lisant 10 fois ses tables qu’on va les mémoriser, et que plus on a de façons de s’en souvenir, plus on ancrera la connaissance.
Il faut aussi se rappeler qu’une multiplication est un « raccourci » d’additions. Au pire, on se débrouillera toujours en faisant des addictions. 3 x 5 = 5 + 5 +5
Les tables de 2, 3, 4 et 5 ne posent souvent pas de problème. Sans parler de la table de 1 et de la table de 10, qui sont pour le coup très sympathique. Je vais parler dans cet article plus précisément des tables de 8 et 9, puis de 7. On verra aussi une technique pour trouver les résultats du produit de 2 nombres compris entre 7 et 9 en utilisant les tables inférieures à 5.
La table de 8
Déjà, on peut remarquer que 8 = 2 x 2 x 2. Multiplier par 8 c’est donc multiplier par 2, puis par 2, puis par 2. Multiplier par 2 c’est ajouter un nombre à lui même, c’est assez facile. 8 x 7 =( (2 x 7 ) x 2) x2 = 14 x 2 = 28 x 2 =56.
Il y a aussi une astuce pour retrouver rapidement la table de 8 :
On écrit en colonne le début de la table, et on tire un trait entre 5 et 6.

Ensuite on complète les dizaines à partir du haut, 0, 1, 2, 3 ,4, et on passe le trait en répétant le 4, puis 5, 6, 7et 8.

Ensuite, en repartant du bas, les unités 0, 2, 4, 6, 8, et 0, 2, 4, 6 et 8. (8 étant pair, dans la table de 8 on n’a que des nombres pairs).

Et voilà, le tour est joué. Avec de l’entrainement, on fait ça très rapidement sur une feuille de brouillon.
La table de 9
Il y a l’astuce des mains. On met ses mains devant soi, paume face à soi. On numérote ses doigts (dans sa tête ou en vrai avec un stylo effaçable).
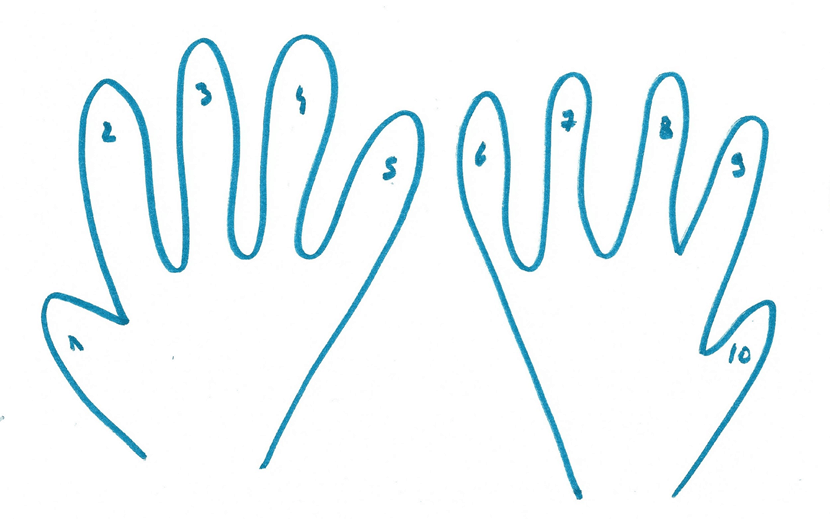
Pour calculer 4 x 9, on va replier le doigt n°4.
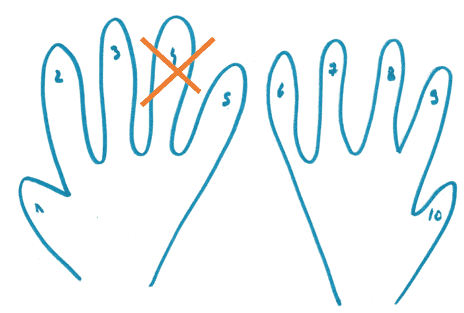
On compte les doigts « avant », ici 3. On compte les doigts « après », ici 6. Le résultat est 36.
Une autre technique, similaire à celle de la table de 8 :

Puis on écrit en colonne les dizaines en partant du haut : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Et ensuite à partir du bas, les unités : 0,1,2,3,4,5,6,7,8,9.

On peut remarquer que la somme des deux chiffres du résultat fait toujours 9. 4 x 9 = 36 et 3+6=9. Cela amorce la notion de critère de divisibilité.
La table de 7
Le problème avec la table de 7, c’est qu’il n’y a pas vraiment grand-chose. C’est là que l’on va utiliser les associations d’idées. Souvent, les produits « qui résistent », ce sont 6 x 7, 7 x 7, 8 x 7. On va les associer pour les retrouver rapidement.
Par exemple, on connait 9 x 7 = 63 grâce au truc de la table de 9. 8 x 7 = 9 x 7 – 7. 63 – 7 cela donne 56.
On peut aussi se raconter une « histoire ». Je vous livre mes propres associations, à vous d’en inventer qui vous parlent.
Pour 8 x 7, j’ai remarqué que les nombres se suivent, si on l’écrit : 56 = 7 x 8. 5,6,7,8.
Pour 6 x 7, je me suis raconté l’histoire suivante « Dieu a crée le monde en 7 jours, à non 6 en fait car il s’est reposé le 7ème jour, donc 42 car 42 c’est la réponse à toutes les questions existentielles de l’Univers ». Pour 42, c’est issu de la culture SF des années années 80, dans le livre de Douglas Adams, le guide du voyager galactique , dans lequel un ordinateur à la question sur « l’univers, la vie et le reste » après un calcul de plusieurs millions d’années répond « 42 ». L’école 42 de Xavier Niel tire son nom de cette légende. Tapez 42 dans la barre de recherche de votre moteur de recherche favori, vous ne serez pas déçu. Vous comprenez avec cette histoire, qu’elle est très personnelle. Et ça marche parfaitement, pour moi.
Si vous êtes en manque d’inspiration pour inventer des histoires, vous pouvez utiliser le livre Les tables de multiplication chez Belin, dans lequel vous trouverez des histoires pour retenir les tables.
Il y a aussi le jeu Multimalin, de Matthieu Protin qui propose des images mentales pour retenir les tables.
Le jeu Tam Tam Multimax est également un bon jeu pour travailler ses tables de multiplication.
Les produit de nombres compris entre 6 et 9 avec les tables de 2, 3, 4 , 5.
Voici une technique qui utilise les mains également, mais elles sont tournées dans l’autre sens.
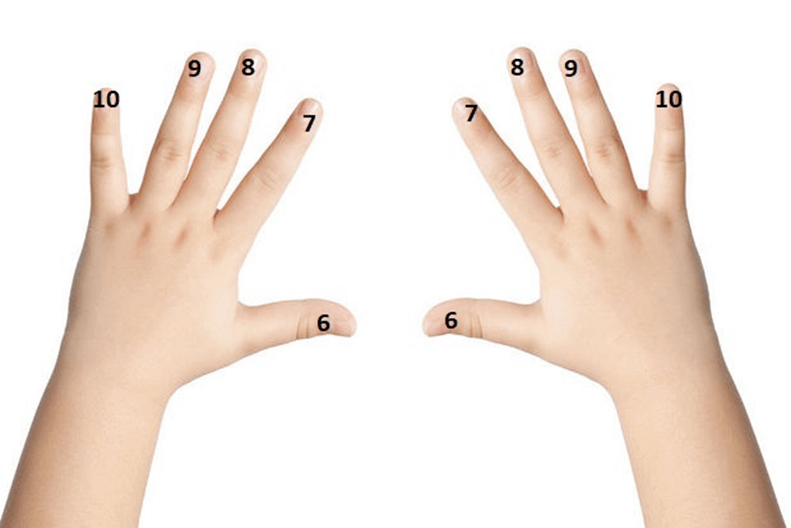
On numérote les doigts comme sur l’image.
Pour effectuer 6 x 7 par exemple, on fait se toucher les doigts 6 de la mains gauche et 7 de la main droite.
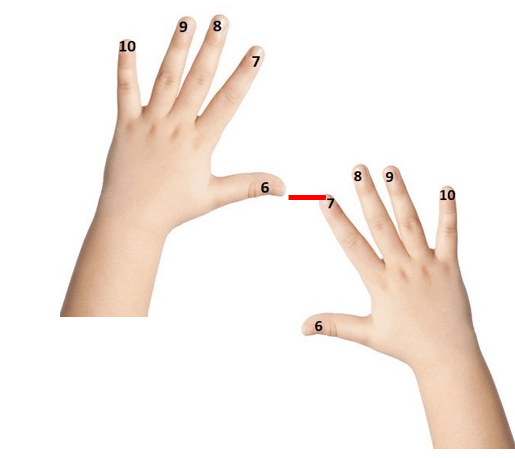
On compte le nombre de doigts qui se touchent et en dessous. Ici il y en a 3, ce sont les dizaines.
On compte ensuite le nombre de doigts « qui restent » dans la main gauche, ici 4, et le nombre de doigts « qui restent » dans la main droite, ici 3. On les multiplie, 3 x 4 =12. On ajoute ensuite les 3 dizaines (30) et 12, ce qui donne 42.
Pourquoi ça marche ?
Un nombre entre 6 et 10 s’écrit 5+a, avec a compris entre 1 et 5.
(5+a) à gauche x(5+b) à droite.
Le nombre de doigts « en dessous » est a+b. On a a+b dizaines c’est-à-dire 10x(a+b).
Le nombre de doigts au dessus est (5-a) à gauche et (5-b) à droite. On calcule (5-a)x(5-b).
On additionne ensuite : 10x(a+b)+(5-a)x(5-b).
Or : 10x(a+b)+(5-a)x(5-b)=10xa+10xb+25-5xa-5xb+axb=25+5xa+5xb+axb.
Et (5+a)x(5+b)=25+5xa+5xb+axb. CQFD !
Pourquoi apprendre les tables à l’ère des machines à calculer ?
Il y a plusieurs raisons à cela.
La première est que cela développe le cerveau. Des connections se créent, la mémoire se développe. On apprend également des méthodes pour mémoriser qu’on pourra réutiliser. On développe l’agilité de son cerveau, et ça servira toute sa vie.
Sur le plan mathématique, apprendre ses tables de multiplications, « dans les 2 sens » (en effet il est tout aussi important, voire plus, d’apprendre que 6 x 7 = 42 que d’apprendre que 42 c’est 6 x 7) , cela donne l’habitude de « décomposer » les objets mathématiques. Cela va servir pour les calculs de fractions, en permettant d’acquérir un mécanisme. Car bien sur, les machines peuvent simplifier et ajouter des fractions, mais quand il y aura des lettres? Les mécanismes ne seront pas acquis. Je le vois tous les jours dans mon cabinet, des élèves de lycée, ayant tellement peu d’habitude en calculs qu’ils se trouvent vraiment en difficulté y compris pour le reste. Cela fait gagner du temps également, les tables de multiplication, et par suite les formules de mathématiques, c’est comme le vocabulaire en anglais. D’ailleurs les mathématiques sont un langage. Imaginez que pour parler anglais, vous deviez chercher chaque mot dans Google trad ? La conversation manquerait de fluidité.
Entretenir ses connaissances
Servez-vous de la table de Pythagore pour identifier précisément les résultats qui vous posent problème, et ceux que vous savez. (Enfin, vos enfants…)
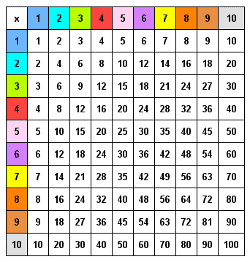
La mémoire est reconstructive, c’est à dire que c’est en se testant que l’on mémorise. Inutile donc de lire plusieurs fois ses tables (ou son cours) pour le mémoriser. Il faut se tester régulièrement. Les jeux de cartes précédemment cités servent à cela. Vous pouvez également vous construire des « flash card », des cartes recto-verso avec d’un côté le produit (6 x 7 par exemple), de l’autre la réponse (42 ici). Vous les stocker dans une boîte et les sortez régulièrement. J’aime aussi beaucoup les mandalas, ou les puzzles. Vous trouverez prochainement dans ma boutique un puzzle mandala que vous pourrez utiliser avec votre enfant.
Un autre genre de mandala se trouve ici, dans le site « la tanière de Kyban », le blog d’un professeur des écoles dans lequel vous trouverez plein d’astuces et d’outils.