Introduction
Imaginons que vous mettiez de l’argent sur un compte épargne, en utilisant le procédé suivant :
La première semaine, vous mettez un euro. La deuxième deux. La troisième trois. Et ainsi de suite. Et, qu’au bout d’un temps infini, votre banquier vous annonce que votre compte épargne est à découvert ! Mais comment est-ce possible ? Cela voudrait dire que 1+2+3+4+5+…+n+… est négatif ?
Plus précisément, 1+2+3+4+…= -1/12 !
Cette formule se trouve dans un des carnets de Srinivasa Ramanujan (1887-1920), il en donne une démonstration et propose un procédé pour donner une valeur à certaines séries « divergentes ».
On aurait plutôt tendance à penser que 1+2+3+4+5+6+7+8+… prend une valeur infinie ou en tout cas très très grande !
Et pourtant…
D’autres avant lui avaient déjà donné une valeur réelle à des séries « divergentes. C’est là que se situe le caractère subversif des mathématiques. En effet, certains mathématiciens n’hésitent pas à remettre en cause l’ordre établi et à ouvrir des passages dans des murs ; par exemple à inventer un nombre dont le carré vaut -1 et créer les nombres complexes, remettre en cause le 5ème postulat de la géométrie d’Euclide et inventer de nouvelles géométries. Mais finalement, n’est-ce pas le propre des mathématiques de « n’avoir peur de rien » et de créer des objets qui à première vue sont contraires aux théories en cours ? Après tout, poser qu’il existe un nombre dont le carré vaut -1 est aussi iconoclaste que de donner une valeur à 1+2+…+n+….
Citons Leonhard Euler (1707-1783), qui avait donné 1-1+1-1+1-1+…+(-1)^n+…=1/2 ; Niels Abel (1802-1829), Émile Borel (1871-1956), Ernesto Césaro (1859-1906) qui ont également travaillé dans le champ des séries divergentes.
Un peu de vocabulaire :
Une série est la somme d’une infinité de termes. Une série est dite convergente quand on obtient à la limite une valeur finie, comme1/2+1/4+1/8+1/16+…=1.
Si la série n’est pas convergente, elle est dite divergente.
Par exemple, la série 1+2+… est divergente et tend vers +∞.
Srinivasa Ramanujan
Qui était Srinivasa Ramanujan ?
C’était sans doute le mathématicien le plus extraordinaire du siècle dernier, et même au-delà.
Il est né en 1887 à Erode, dans le sud de l’Inde, dans une famille de brahmanes, pauvre et pieuse. Il n’a qu’une seule passion, les mathématiques. C’est en particulier un calculateur hors pair. Tout jeune, il est fasciné par le nombre π et en apprend un très grand nombre de décimales.
On peut aisément imaginer que ses camarades de classe ne le comprennent pas, et qu’il n’ait pas beaucoup d’amis. Ce sera d’ailleurs une des grandes caractéristiques de sa vie, sa solitude intellectuelle, parce que, à part les mathématiques, il ne s’intéresse à rien, et que personne ne saisit vraiment ce qu’il énonce.
Il est tout à fait autodidacte, dévorant seul et très jeune des livres de mathématiques ardus. Il note très tôt de magnifiques formules de mathématiques dans des carnets, en élaborant parfois des idées de démonstration. Mais les démonstrations, ce n’est pas ce qui le passionne. Ramanujan affirme rêver de ces formules pendant la nuit et les noter à son réveil le matin. Il prétend qu’elles lui sont inspirées par la déesse Tamagiri – rappelons qu’il est très pieux.
Il suit plutôt médiocrement des études, qu’il n’achèvera pas, à cause de sa passion exclusive pour les méthématiques, et après avoir écrit un ou deux articles pour la revue de la société mathématique indienne, se voit contraint d’accepter un travail alimentaire de comptable. Il a toujours un carnet avec lui, dans lequel les autres le voient écrire fiévreusement dès qu’il a un moment.
Voici un exemple de formule qu’il voit « en rêve » :
Incité par un de ses collègues anglais, il écrit plusieurs lettres à des mathématiciens anglais, qui restent sans réponse. En 1913, il a la bonne idée d’écrire à G.H.Hardy.
G.H Hardy, (1877-1947), est un mathématicien anglais, grand spécialiste de la théorie des nombres. En 1913, il est professeur à Cambridge, membre de la Royal Society, auteur réputé en mathématiques.
Voici ce qu’Hardy raconte (extrait tiré de son livre Apologie d’un mathématicien[1]) quand il reçoit la lettre de Ramanujan, contenant plusieurs de ses formules.
J’aimerais que vous commenciez par essayer d’imaginer la réaction immédiate d’un banal professeur de mathématiques (sic) à la lecture d’une lettre comme celle-ci, sachant qu’elle émane d’un obscur employé indien.
Voici quelques-unes des formules contenues dans la lettre :

Hardy explique ensuite qu’il a essayé de « s’y reconnaître un tant soit peu », parmi les formules proposées.
« J’avais moi-même déjà démontré des choses comme en (1.7), et (1.8) me disait vaguement quelque chose. […]. J’ai estimé qu’en ma qualité de spécialiste des intégrales définies, je pouvais sans doute démontrer (1.5) et (1.6), ce que j’ai fait, au prix de bien plus d’embarras que je m’y étais attendu. […] Les formules (1.10) et (1.13) se situent à un autre niveau ; elles sont toutes deux, à l’évidence, difficiles et profondes […]. (1.10) et (1.12) me dépassèrent complètement ; je n’avais jamais vu auparavant quelque chose qui s’en approchât, même de loin. Il suffisait d’un coup d’œil pour se rendre compte qu’elles n’avaient pu être écrites que par un mathématicien de tout premier rang.»
C’est dire le génie de Ramanujan, parce qu’Hardy, c’est quand même LE spécialiste en la matière !
Hardy a eu ensuite cette phrase restée célèbre « ces formules sont sûrement vraies, car si elles ne l’étaient pas, personne n’aurait pu avoir assez d’imagination pour les inventer ».
Hardy prend donc Ramanujan très au sérieux et réussit à le convaincre de venir travailler avec lui en Angleterre. Il arrive à Londres, en 1914, ce qui n’est pas la meilleure période… De constitution fragile, souffrant des privations dues à la guerre, Ramanujan a de gros soucis de santé. Il repart en Inde pour y mourir en 1919, dans sa trente troisième année.
Ramanujan a laissé trois carnets de formules, plus des pages libres retrouvées par hasard bien plus tard (en 1976) -le quatrième carnet-, soit plus de 4500 formules, dont la dernière a été démontrée en 2019. Moins d’une demi-douzaine comportent des erreurs.
Hardy avait une très haute estime pour Ramanujan. Un exemple : Hardy avait son propre système de notation des mathématiciens. Il les notait de 1 à 100, à lui-même il s’attribuait la note de 25, à son collègue Littlewood 30, à Hilbert 80 et à Ramanujan… 100.
Terence Tao, mathématicien australien, né en 1975 et médaillé en Fields en 2006, et qui sait de quoi il parle, a dit de Ramanujan :
« Son talent était exceptionnellement hors du commun, et il est l’un des rares mathématiciens contemporains que je qualifierais de génie au sens populaire du terme. »
Srinivasa Ramanujan reste un mystère. D’où lui venaient ses formules ? Comment se fait-il que certains êtres humains soient tellement en avance sur le temps que personne ne les comprend à leur époque ?
Quelques calculs
Il existe donc de nombreuses façons rigoureuses de définir une valeur pour une série divergente. Nous ne rentrerons pas dans les détails techniques ici. Notons que, quand nous attribuons des valeurs aux séries divergentes, nous nous plaçons dans un cadre théorique qui n’est pas le cadre classique de la théorie des séries convergentes.
Il est à noter que ces différents procédés marchent aussi si la série est convergente au sens classique, qu’ils ne se contredisent pas entre eux – il se peut qu’un procédé ne permette pas d’attribuer une valeur et qu’un autre si, mais si deux procédés distincts permettent d’attribuer une valeur, ce sera la même- et que tous ces procédés conservent les propriétés de calculs habituelles, dont nous allons nous servir dans les calculs qui suivent.
Nous allons faire les calculs en admettant que les différentes sommes infinies ont une valeur.
Calcul de C=1-1+1-1+1-1+….
On a C=1-C. Donc 2C=1, ce qui donne C=1/2.
Calcul de S=1-2+3-4+5-6+….
S= 1-2+3-4+5-6+….
-C=-1+1-1+1-1+1 -…
Donc S-C= (1-1)-(2-1)+(3-1)-(4-1)+(5-1)-(6-1)+….=-1+2-3+4-5+…= -S
On a alors 2S=C=1/2, d’où S=1/4.
Calcul de R=1+2+3+4+5+4+….
On a :
R = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 +9+10+…
4R= 4+ 8+ 12+ 16 + 20+…
On a noté les nombres de la série 4C en dessous des nombres pairs de la série R.
On soustrait 4R à R, en regroupant les calculs « colonnes par colonnes ».
On obtient :
-3R= 1-2+3-4+5-6+7-8+9-10+…, soit S.
On a donc -3R=S, ce qui donne R=-1/12.
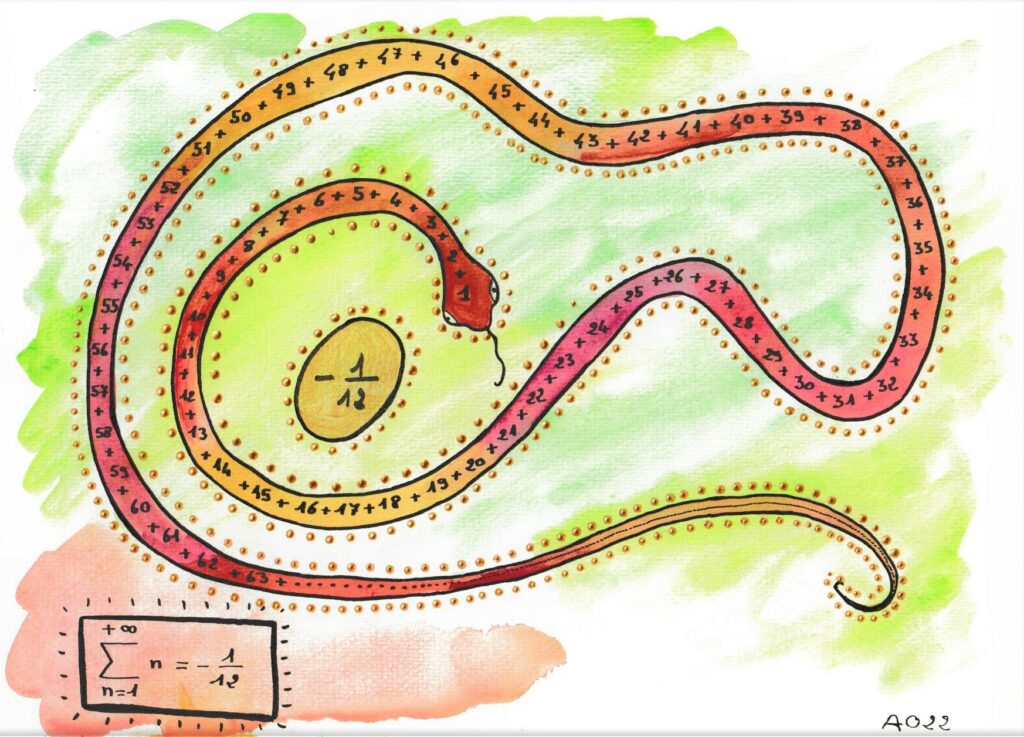
Mais à quoi cela peut-il servir ?
Il se trouve que cette formule paradoxale a permis d’élaborer une théorie de physique quantique, qui a été validée par l’expérience.
Il s’agit de ce que l’on appelle « l’effet Casimir ».
Hendrik Casimir, physicien néerlandais (1909-2000), s’est intéressé en 1948, à la force attractive entre deux plaques parallèles conductrices et non chargées, dans le cadre de la mécanique quantique. Il élabore une théorie, fait des calculs et tombe… sur la somme 1+2+3+4+5+6+…, qui est divergente au sens classique et tend même très grossièrement vers +∞, comme nous l’avons expliqué en introduction. Il a d’abord envisagé s’être trompé, ou que sa théorie était bonne à mettre à la poubelle. Mais il avait entendu parler de cette valeur paradoxale de -1/12. Il a donc remplacé dans ses calculs cette somme par -1/12 et a continué. Il a pu ainsi élaborer sa théorie. Une théorie physique bien sûr n’a pas d’intérêt si elle n’est pas validée par l’expérience. Et, fait remarquable, elle a bien été validée par l’expérience ! Ce qui prouve qu’elle est cohérente et juste (jusqu’à ce que bien sûr, on trouve plus tard une autre théorie qui l’affine et l’englobe).
C’est sans doute ce à quoi on peut penser en parlant, avec Eugène Wigner (physicien hongrois (1902-1995), de « la redoutable efficacité des mathématiques ».
Comme quoi, on ne peut jamais savoir « à quoi vont servir » les mathématiques.
[1] Edité chez Belin. Les extraits qui suivent ainsi que les formules sont également tirés de ce livre.