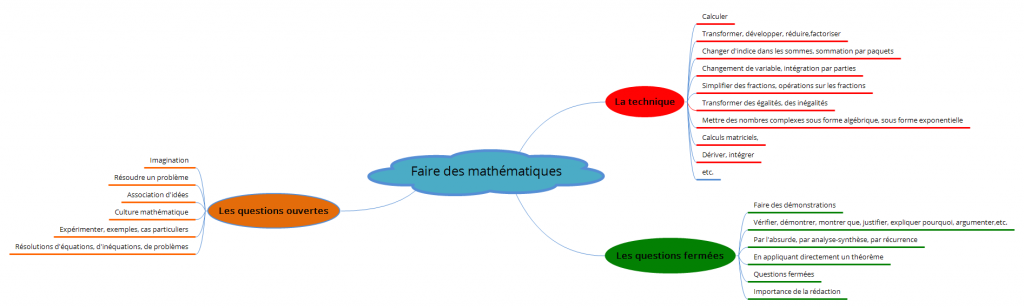
Dans la pratique des mathématiques, on peut distinguer trois types de situations.
Les questions techniques, les questions fermées, les questions ouvertes.
Ces trois types d’activités peuvent se travailler de manière indépendante, et nécessitent des compétences différentes. En classes préparatoires, les questions techniques et les questions fermées sont plutôt présentes à l’écrit et les questions ouvertes plutôt à l’oral. Bien sûr, la technique n’étant pas une fin en soi, cette compétence est utilisée tout le temps.
La technique.
Tout ce qui est technique, faire des calculs, nécessite de l’attention, de l’entraînement, de l’organisation et aussi une bonne gestion du stress. En effet, si on veut être efficace dans un calcul, il ne faut surtout pas se précipiter, c’est à ce moment-là que l’on fait des erreurs. Il s’agit de mettre en pratique la maxime « festina lente », « hâte-toi lentement » de l’antiquité. Il est primordial de bien connaître et comprendre les règles utilisées .
- Quand on « barre » dans une simplification, on fait quoi ? Quand on « fait passer de l’autre côté d’une égalité ou inégalité » on fait quelle opération ? Quand on « distribue un signe», il ne s’agit pas de « changer les signes dans la parenthèse », sinon –(3-x) devient 3+x. Il faut observer l’expression avant de se précipiter dans une transformation (typiquement pour réduire une somme de fractions au même dénominateur, observer les dénominateurs pour chercher le dénominateur commun le plus petit possible, et regarder s’il n’y a pas au préalable des simplifications possibles.
Il est nécessaire de savoir aussi dans quel but on fait un calcul (si par exemple c’est pour étudier le signe d’une expression, il vaut mieux factoriser), ainsi que les « formes canoniques » attendues. Un polynôme on l’écrira en général, soit sous forme développée et réduite, soit sous forme factorisée, mais pas x(x^2+3)-5.
Quand on a une expression assez longue à transformer, il est plus efficace de faire des « sous-calculs », de calculer des petits bouts de l’expression et de réinjecter la nouvelle forme dans l’expression initiale, plutôt que de tout recopier à chaque fois, ce qui multiplie les risques d’erreurs. Cela développe d’ailleurs le sens de l’organisation.
Pour être à l’aise en calcul, il n’y a pas d’autre solution que la répétition, l’entraînement régulier. L’idéal c’est d’en faire un peu chaque jour, en réfléchissant bien à chaque fois aux règles de calculs employées. C’est comme faire des gammes en musique, ou répéter un geste technique en sport.
Les questions fermées.
Une question fermée (que ce soit une démonstration d’un théorème du cours ou un exercice), c’est une question dont on a la réponse. Par exemple « montrer que pour tout x réel, x^2+x+1 est positif », par opposition à « quel est le signe de x^2+x+1 ? ». Ou « montrer que la suite (u_n) est croissante », par opposition à « étudier la monotonie de la suite ». On sait d’où on part (les hypothèses) et où on arrive (le but). Reste à trouver le chemin. C’est l’observation du but qui va nous permettre de mettre en place une stratégie. Une erreur classique consiste à « partir » de l’hypothèse.
(Par exemple dans la question « montrer que si la suite (u_n) tend vers L et si f est une fonction continue en L, alors la suite (f(u_n)) tend vers f(L) », il ne faut pas commencer par écrire « ce que veut dire (u_n) tend vers L », mais se demander, « comment je vais faire pour démontrer que la suite (f(u_n)) tend vers f(L) ? ». )
Il faut observer le but en se posant plusieurs questions (faire des mathématiques, c’est se poser des questions, tout le temps !)
- A quelle partie du cours ce problème fait-il référence ?
- Quelle est la définition ?
- Est-ce que je connais un théorème dont la conclusion ressemble à mon but ?
- Est-ce que j’ai déjà rencontrée une situation analogue et qu’est-ce qu’on a fait à ce moment-là ?
La rédaction d’une démonstration est très structurée. Si on suit les principes, on ne peut pas faire de fausses démonstrations (on peut ne pas aboutir, mais ça c’est une autre histoire).
Un théorème, une propriété (ce que nous appellerons un « outil ») se présente toujours de la même façon : « Si H alors C », H étant un ensemble d’hypothèses et C la conclusion. Il y a plusieurs écritures synonymes, il faut repérer cette structure. Et bien apprendre les hypothèses quand on apprend un théorème !!!!
Différentes écritures du même théorème :
- Si (u_n) est une suite croissante et majorée, alors elle converge
- Soit (u_n) une suite croissante et majorée. (u_n) est convegente.
- Une suite croissante et majorée converge.
Pour utiliser un théorème, on doit d’abord s’assurer que les hypothèses sont validées.
On peut alors écrire « donc » et invoquer le théorème («donc, d’après le théirème nom_du_théorème », donc, d’après le théorème qui dit que si.. alors…, s’il n’a pas de nom, mais c’est plus ennuyeux) et en tirer la conclusion.
Le schéma du principe est :
H
Si H alors C
————–
Donc C
Bien sûr, dans une démonstration, on peut utiliser plusieurs théorèmes. L’art consiste à faire le lien entre les hypothèses données dans l’énoncé et les hypothèses nécessaires pour appliquer le théorème.
Se pose aussi la question du détail de la rédaction. Il est clair que si on a l’égalité x +2=3 et qu’on en déduit x=-1, on ne va pas le justifier sur une copie (c’est-à-dire expliciter le théorème utilisé), sinon on n’en finirait plus. Mais, pour soi, il est important de savoir quelle propriété, règle ou théorème on utilise.
En mathématique, il n’y a pas d’argument d’autorité. Tout peut se justifier.
On peut se fixer comme règle de conduite qu’on rédige non pas pour le professeur, mais pour un camarade de sa classe qui a acquis les notions des classes précédentes mais qui a besoin qu’on lui détaille les notions nouvelles vues en cours.
Les questions ouvertes.
C’est l’activité mathématique qui demande le plus d’imagination, puisqu’on ne sait pas quelle peut être la conclusion. (Cette suite est-elle convergente ?, l’équation a-t-elle des solutions, lesquelles ? etc.) En CPGE, ce sont plutôt des questions posées à l’oral.
Une première stratégie consiste à se faire une idée du résultat et à transformer le problème en « démonstration ». Si on nous demande si une suite converge ou pas, on peut par exemple conjecturer que oui et transformer la question en « montrer que la suite converge ». Si on n’y arrive pas, on peut alors tester l’autre possibilité, et transformer le problème en « montrer que la suite diverge ».
C’est là que l’expérimentation est importante. En mathématiques cela passe par
- Regarder des cas particuliers
- Faire des dessins
- Utiliser sa calculatrice pour faire des conjectures
- Puiser dans sa « culture mathématique » (est-ce j’ai déjà rencontré une situation similaire ?
Il est important de bien maîtriser les concepts, afin de savoir ce que l’on peut faire ou pas, afin de transformer le problème en un problème qu’on sait résoudre. Par exemple, si on nous demande de résoudre l’équation e^x+e^-x=3, vu que « en gros » on sait résoudre des équations du premier ou du second degré, ou des équations du type « e^x=c », on va transformer le problème en (e^x)^2-3(e^x) +1=0, poser z=e^x, résoudre l’équation du second degré z^2-3z+1=0, puis les équations e^x=s, où s est une solution de l’équation précédente.
Quelques citations sur le savoir, qui sont très pertinentes pour le cours de maths !
- Mieux vaut ignorer une chose que de la savoir mal.(Publiusus Syrus, 1er s av JC)
- Mieux vaut savoir relativement peu mais avoir bien appris le peu que l’on sait. (Edouard Herriot 1919)
- C’est savoir quelque chose que de savoir ce que l’on ignore. (Jean Stobbée 5ème s ap JC)
- Mieux vaut savoir bien que savoir beaucoup, mieux vaut ne rien savoir que de savoir mal. (André Grétry 1801)