11 clés et 1 conseil pour optimiser les révisions du bac en maths
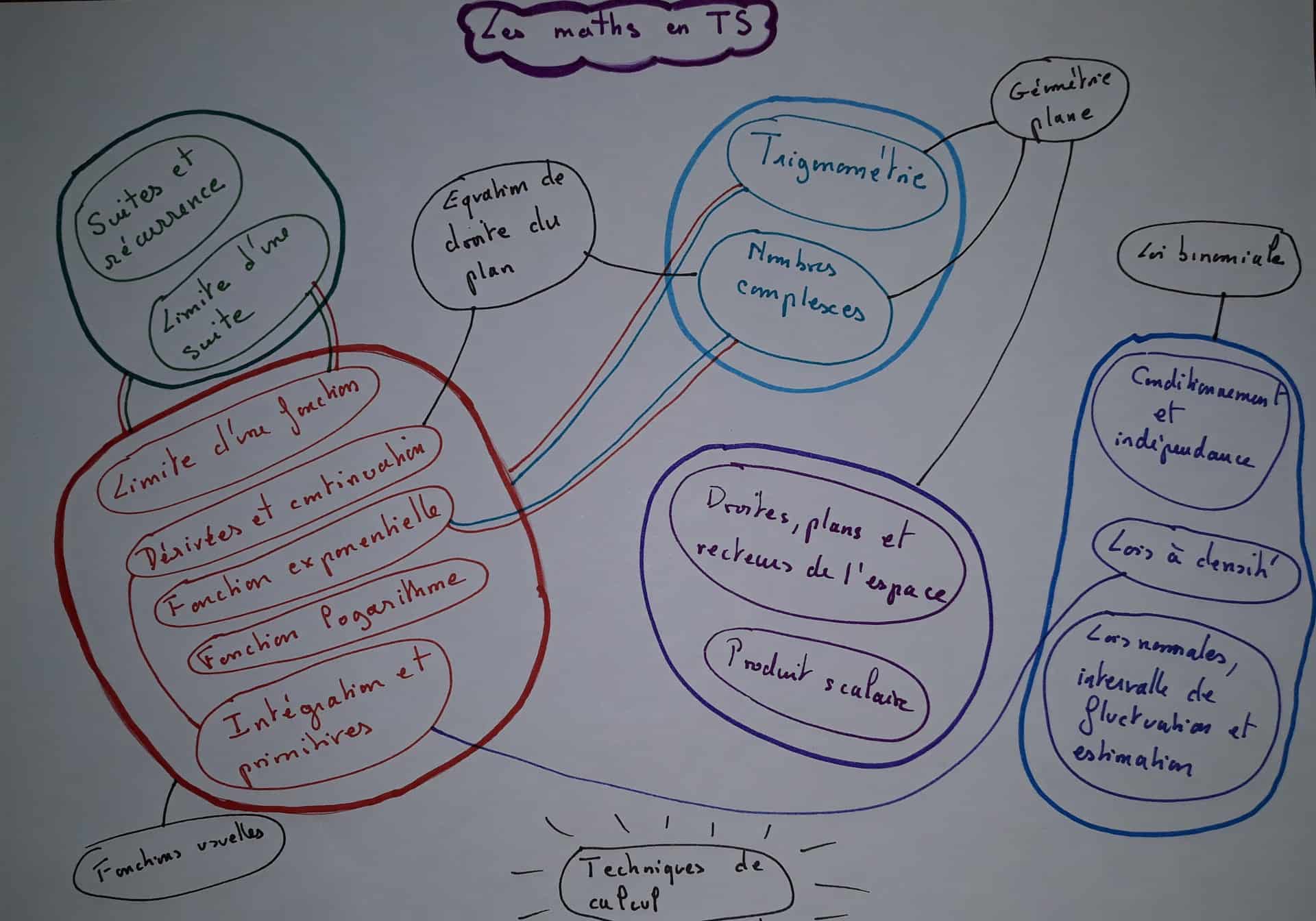
- Fais une carte mentale du cours de maths, en regroupant les différents chapitres qui portent sur le même thème, et en établissant des liens entre les chapitres. Commence par prendre une feuille, format A4 paysage, et sans regarder ton livre ni ton cours, écris les titres des chapitres que tu as étudié. Commence à les regrouper par « genre ». Ensuite, tu ouvres ton livre et tu regardes la table des matières, vérifie que tu n’as rien oublié. Utilise des couleurs pour les chapitres qui vont ensemble. Pour le cours de TS ça donne ceci par exemple (mais le mieux c’est de la faire toi-même).
- Pour chaque chapitre, fais une fiche-résumé. Tu peux utiliser ces 5 questions, que j’ai adaptées pour les mathématiques (inspirées du livre de Guy Sonnois, Accompagner le travail des adolescents avec la gestion mentale, chez Chronique Sociale)
- Qu’est-ce que c’est ? De manière informelle, et la définition mathématique. Comment je me le représente ?
- Quelles sont les notions dont j’ai besoin avant pour ce chapitre ?
- A quoi ça me fait penser ? (en maths ou en dehors des maths). Est-ce que cette association d’idée m’aide ou me perturbe ?
- Qu’est-ce qu’on fait avec, quelles sont les propriétés de base ? A quelles questions elles permettent de répondre ? A quoi cela sert de le savoir ?
- Comment est construit un problème sur ce thème ?
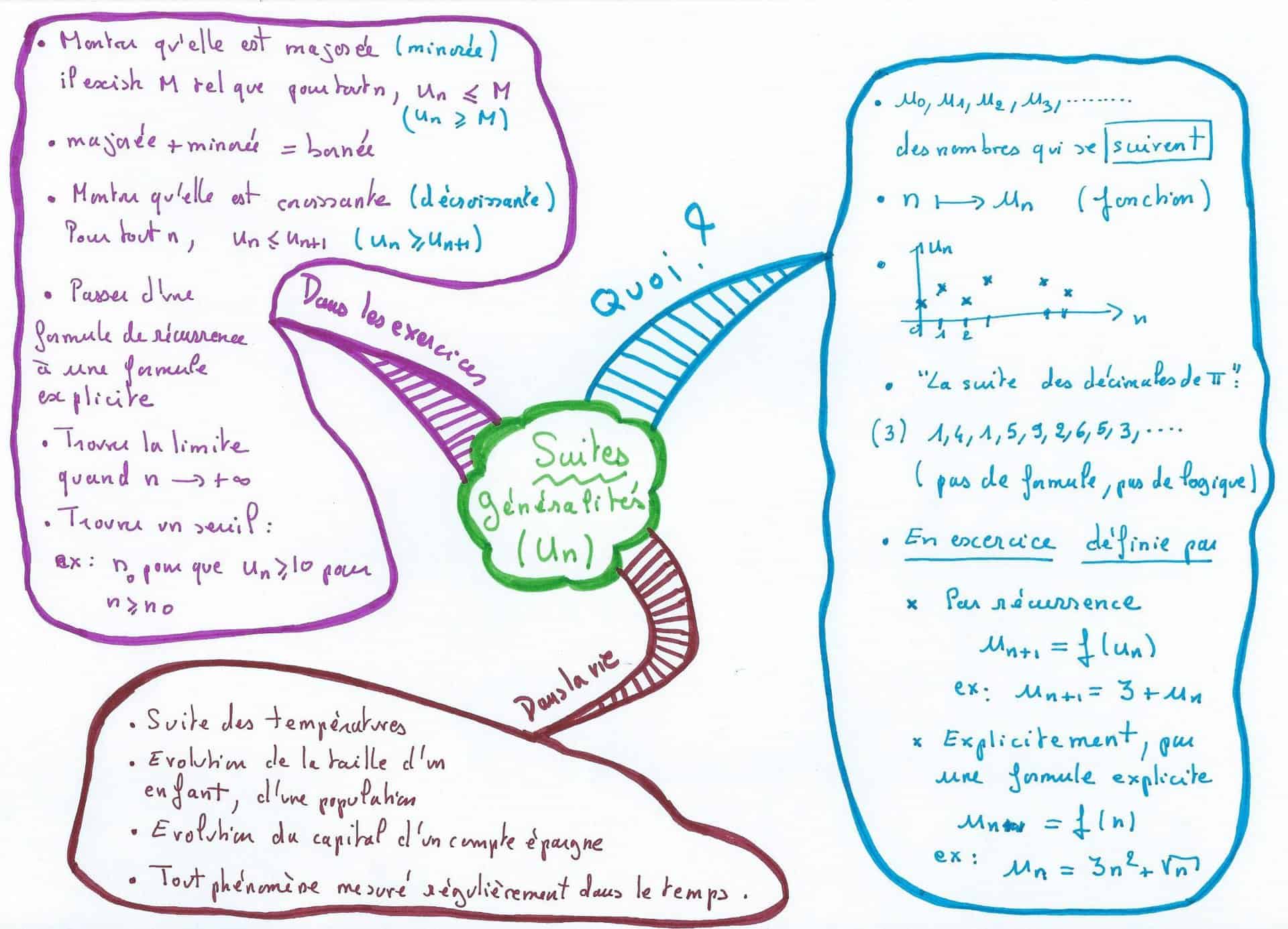
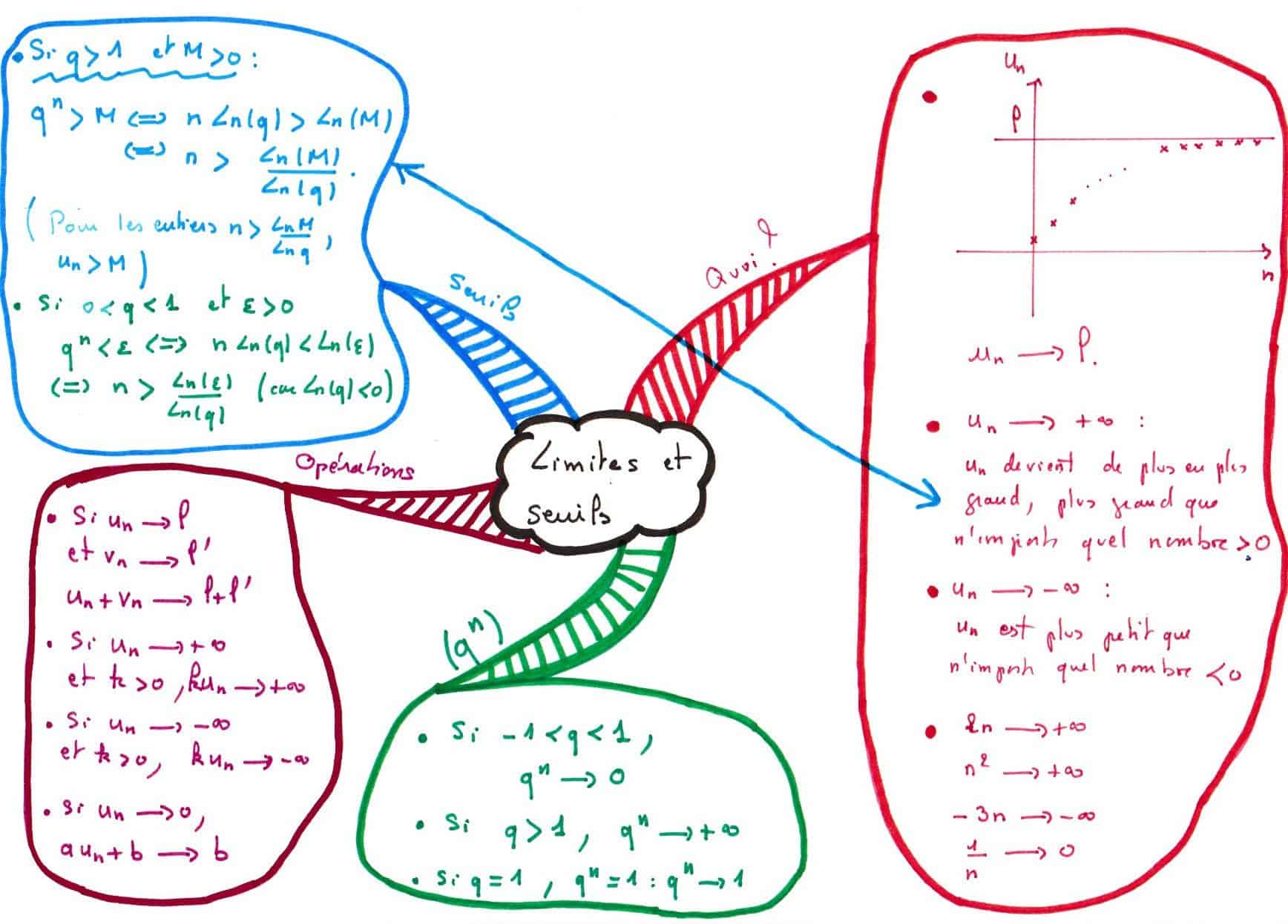
Voici une carte mentale sur les suites numériques, et une sur les limites des suites.
- Imagine une liste de questions que tu poserais à un camarade pour savoir s’il connait son cours. Ecris sur une feuille les questions et en face les réponses, ou sur des petites fiches, la question d’un côté la réponse de l’autre. Fais ça aussi pour les formules.
Pour réviser, tu caches les réponses, et tu réponds. Tu peux même faire le contraire, regarde les réponses et essaie de retrouver la question.Voici une liste de questions sur les suites:- Quels sont les deux modes de génération d’une suite ?
- Comment on calcule des termes d’une suite ?
- Suite arithmétique (géométrique) définition ?
- Suite arithmétique (géométrique) formule ?
- Somme de termes consécutifs d’une suite arithmétique (géométrique)
- Définition d’une suite croissante (décroissante)
- Comment on peut utiliser l’information que la suite est croissante ou décroissante
- La notion de limite.
- Limite des suites usuelles
- Opérations sur les limites
- Cas des formes indéterminées
- Limite des suites monotones
- Théorème des gendarmes
- Principe de la démonstration par récurrence.
- Algorithmes de calculs, algorithmes de seuil.
- Le soir, avant de t’endormir, choisis un thème et récapitule tout ce que tu sais. Demande-toi ce que tu as appris aujourd’hui. Pendant ton sommeil, le cerveau trie les informations. Dans le processus d’apprentissage, le sommeil est primordial. De plus, quand on est fatigué, on n’arrive pas à réfléchir.
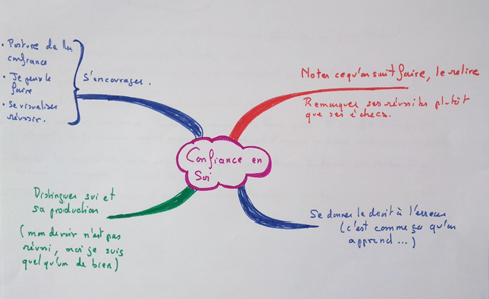
- Pour booster ta confiance: fais-toi un « petit cahier de tes savoir-faire ». (Je sais dériver une fonction, je sais rédiger une récurrence, je sais résoudre une équation du second degré même quand le discriminant est négatif…). Relis-le régulièrement.Voici d’autres idées pour développer ta confiance en toi :
- Dans chaque programme, il y a quelques « gros théorèmes », pour les quels il y a une rédaction spécifique à apprendre. Par exemple, le théorème des valeurs intermédiaires et son corollaire, la démonstration par récurrence, la démonstration que c’est une loi binomiale…
Observe les exercices et trouve les points communs dans la rédaction des questions, les indices qui devront te faire penser à ce théorème. Pour le théorème des valeurs intermédiaires, en général, la question ressemble à « montrer qu’il existe un réel a vérifiant une certaine équation, et dans la question qui suit on te demande de trouver une valeur approchée. Pense à mettre l’équation sous la forme « f(x)=0 », et à utiliser un tableau de variation (qu’on t’a fait faire la question d’avant…) - Si tu as besoin de bouger quand tu travailles: mets l’énoncé à un endroit, et va écrire la résolution à un autre endroit. Sur un tableau blanc ou un paper-board c’est encore mieux. En plus cela fait travailler sa mémoire à court terme.
- Le temps de concentration est limité. Fais des pauses régulières, toutes les 25 minutes par exemple. Une pause où tu vas bouger un peu (va boire un verre d’eau par exemple). Aide-toi d’un chronomètre. Tu peux utiliser différentes applis, qui t’empêcheront d’aller sur ton téléphone en plus (Forest ou Pomodoro). Attention à minuter ta pause aussi ! 5 minutes, pas plus.
- Utilise tes fiches quand tu fais un exercice, et à la fin, demande-toi ce que cet exercice t’a fait travailler, si tu pourrais le généraliser. Fais un résumé des outils mathématiques utilisés. Essaie d’en inventer un du même genre. En utilisant tes fiches, tu apprends à associer l’énoncé, l’exercice, avec le cours, et tu apprends ton cours en plus.
Tu peux aussi commencer à réviser à partir d’exercices. Mais dans ce cas, il ta faut alors aller voir le cours correspondant et en faire une fiche. - Fais des calculs tous les jours ! Au moins 10 minutes. Des calculs de toutes sortes : résoudre des équations, résoudre des systèmes, calculer des dérivées, des primitives. Des calculs de fractions, de puissances, de racines carrées. Des transformations d’exponentielles ou de logarithmes… (Tu peux voir mon ancien article ici).
C’est l’entraînement qui te permettra de gagner en fluidité, de gagner du temps, de te sentir à l’aise.
Apprends à te vérifier.
Utilise tes fiches formules pour faire les calculs. Tu les apprendras en même temps. - Si tu veux faire des mathématiques après le bac, dans tes études, alors, avant de travailler, dis-toi que tu apprends et tu travailles pour l’an prochain aussi ! Si tu apprends pour l’épreuve du bac, une fois celle-ci passée, tu l’oublieras ! (Et c’est bien normal, c’est comme cela que le cerveau fonctionne.)
Cesse tes révisions le week-end avant les épreuves ! Tu as besoin d’arriver avec envie. Si tu es saturé, tu seras moins performant. Donc repos total samedi 15 et dimanche 16 juin.

7 conseils pour le jour J
- Tu reçois ton sujet : Commence par respirer ! Mets tes mains à plat sur la table, ferme les yeux et concentre- toi sur tes ressentis physiques (quelle est la sensation de mes mains sur la table, de mes pieds par terre, est-ce que je tremble, est-ce que j’ai la gorge serrée, etc.) Bois un peu d’eau. (pense à prendre une gourde !)
- Prend une feuille de brouillon, regarde brièvement les exercices, résume-les par un ou deux mots : Nombres complexes, proba, géométrie, etc. et met en face le nombre de points. Prévois une répartition en gros de ton temps, en te laissant 15 min de marge. Ensuite, choisis un ordre en fonction de tes goûts et lance-toi. Ne reste pas trop longtemps sur une question que tu ne sais pas faire. Avance, tu pourras y revenir plus tard. Surveille ton temps, mais si tu es en plein milieu d’une question, finis de la rédiger avant de passer à l’autre exercice.
- Face à un exercice, (par exemple « les nombres complexes »), commence par prendre quelques minutes pour te rappeler ce que tu sais à ce sujet, en repensant à tes fiches. S’il y a des formules particulières que tu as peur d’oublier, tu peux les écrire au brouillon.
- Pour chaque question, commence par élaborer une ou plusieurs stratégies. Il faut apprendre à résister à sa première idée. (Ce n’est pas parce qu’on voit un trinôme du second degré qu’il faut forcément calculer le discriminant et les racines). Pour élaborer ta stratégie, n’essaie pas de penser à transposer un exercice qui ressemble, mais pose-toi la question des « définitions » pour commencer. (Si on te demande de montrer qu’une suite est croissante, rappelle-toi la définition, et réfléchis à plusieurs stratégies). Essaie d’élaborer au moins deux stratégies, puis tu en choisis une, en fonction du contexte. Avant de te lancer dans un calcul long, demande-toi à quoi ça va te servir quand tu l’auras fini.
Bref, pose-toi des questions ! C’est comme cela que tu auras les réponses. - L’énoncé est ton ami ! Regarde si tes résultats sont cohérents, regarde si tu n’as pas la réponse quelques question plus loin. Si tu es bloqué, souvent c’est parce qu’il y a un indice dans l’énoncé que tu n’as pas utilisé.
- Les calculs:
- Si tu dois faire un calcul, distingue si c’est une question « ouverte », où la réponse n’est pas donnée (quelle est la limite de la suite ? Déterminer la dérivée, etc…) ou une question « fermée », dans laquelle la réponse est donnée (Montrer que x^2+5x+6=(x+2)(x+3),…).
- Dans ce deuxième cas, il est parfois plus simple de partir du membre de droite.
- Si on te demande de « vérifier » qu’un certain nombre est solution d’une équation, pas la peine de chercher à résoudre l’équation, il suffit de remplacer.
- Demande-toi aussi pour quoi tu fais un calcul, dans quel but dans l’exercice, ça te donne des idées pour le faire (par exemple une dérivée, il est préférable de l’avoir sous forme factorisée pour étudier le signe plus simplement).
- Pense à simplifier les fractions.
- Fais des calculs intermédiaires.
- Vérifie tes calculs !
- Pour ne pas faire d’erreurs de calculs, ne saute pas d’étapes.
- Fais très attention à la rédaction !
-
- N’oublie pas que tu ne rédiges ni pour toi, ni pour ton professeur, ni même pour un autre professeur (même si en vrai, c’est un professeur qui va lire ta copie et la noter). Imagine plutôt que tu rédiges pour un camarade, qui n’a aucune initiative. Il faut lui expliquer ta démarche à chaque fois, et pourquoi c’est légitime d’utiliser tel ou tel théorème. La rédaction est toujours la même : « j’ai ces propriétés qui sont vérifiées (les hypothèses du thm), j’ai ce thm (l’outil), donc, je peux en tirer cette conclusion ».
- Fais attention quand tu écris « donc ». Il faut qu’il y ait un lien de cause à effet. Par exemple, cette phrase : « il fait soleil donc le hamburger coute 5 euros » n’a aucun sens mathématique, même s’il fait vraiment soleil et que le hamburger coûte vraiment 5 euros.
- Fais bien attention à répondre à la question posée, dans les termes où elle est posée. Par exemple, si on te demande les cordonnées d’un point, une fois tes différents calculs terminés, tu dois écrire : « M(4 ;5) », ou « les coordonnes de M sont (4 ;5) ». Et encadre le résultat. (Cela te permet de bien vérifier que tu réponds à la question pose, et c’est plus agréable pour le correcteur.)
- N’oublie pas les barres de fractions, ni le cadre et les lignes dans un tableau de variation (c’est super énervant quand on corrige).
- Utilise tout le temps de l’épreuve! Relis-toi, corrige tes fautes d’orthographe, encadre tes résultats, sépare les questions par des lignes horizontales. La présentation est importante. Pense que le correcteur a beaucoup de copies à corriger, en peu de temps, et que personne n’aime corriger des copies ! Alors, sois sympa avec lui !
-