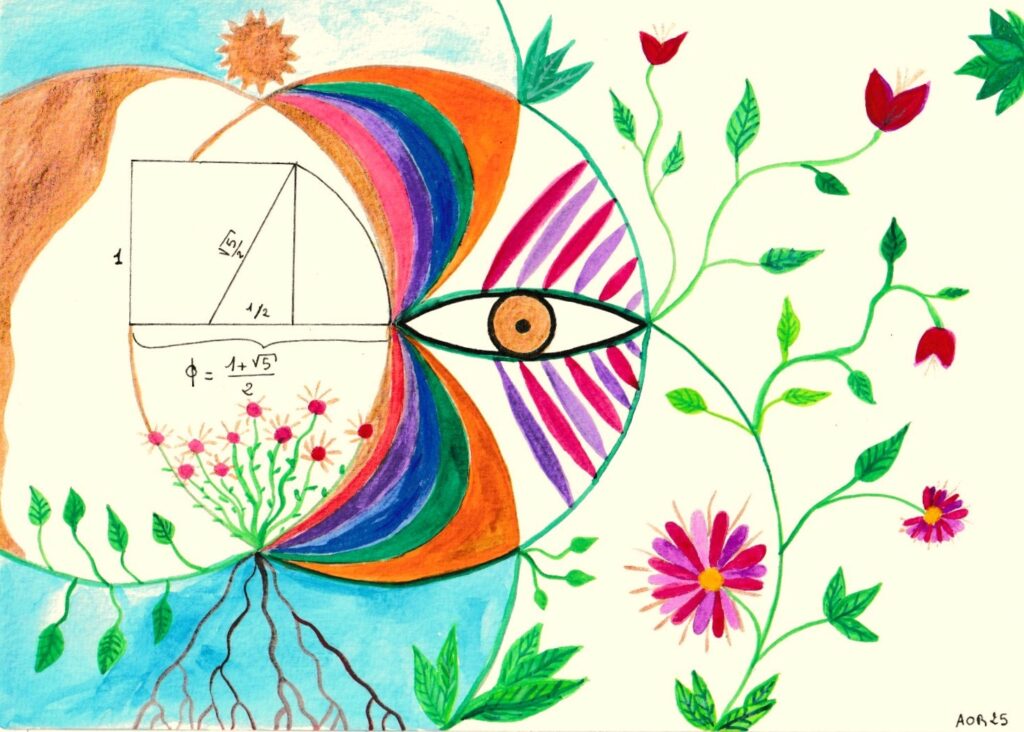Ces deux nombres vous disent certainement quelque chose, et pour cause, c’est le format d’une feuille A4. Mais pourquoi ces mesures bizarres ? Pourquoi pas 20 cm x 30 cm par exemple ?
L’observation
Vous savez qu’il y a plusieurs formats de feuilles dans la série A. Pour être précis, cela va de A0 à A10. Plus le nombre est grand, plus la feuille est petite (encore une bizarrerie). En fait, le nombre après indique le nombre de pliages à partir de la feuille initiale. A0 c’est le format de départ (0 pliage), A1 obtenu après un pliage, A2, deux, etc.
Le point important, c’est qu’à chaque fois la proportion est la même. Je m’explique :
Si je considère un rectangle de largeur m et de longueur L, la proportion sera le rapport L/m.
Dans le cas du format A4, la proportion est donc 29,7/21, soit 1,4128…
Le format d’une feuille A3 est 42 cm x 29,7 cm. La proportion est 42/29,7, soit 1,414141…
Le format d’une feuille A5 est 21 cm x 14,8 cm. La proportion est 21/14,8, soit 1,4189189…
On remarque, si on arrondit à deux chiffres après la virgule, ce qui n’est pas insensé car je ne pense pas que l’oeil humain puisse percevoir au delà, on obtient à chaque fois 1,41, soit la même chose.
Je vous laisse vérifier avec tous les formats A.
L’explication mathématique
Pour obtenir les différents formats A, on part d’une feuille rectangulaire (A0), qu’on plie en 2, on obtient deux feuilles A1. On repart d’une feuille A1 qu’on plie en deux, pour obtenir deux feuilles A2, etc.
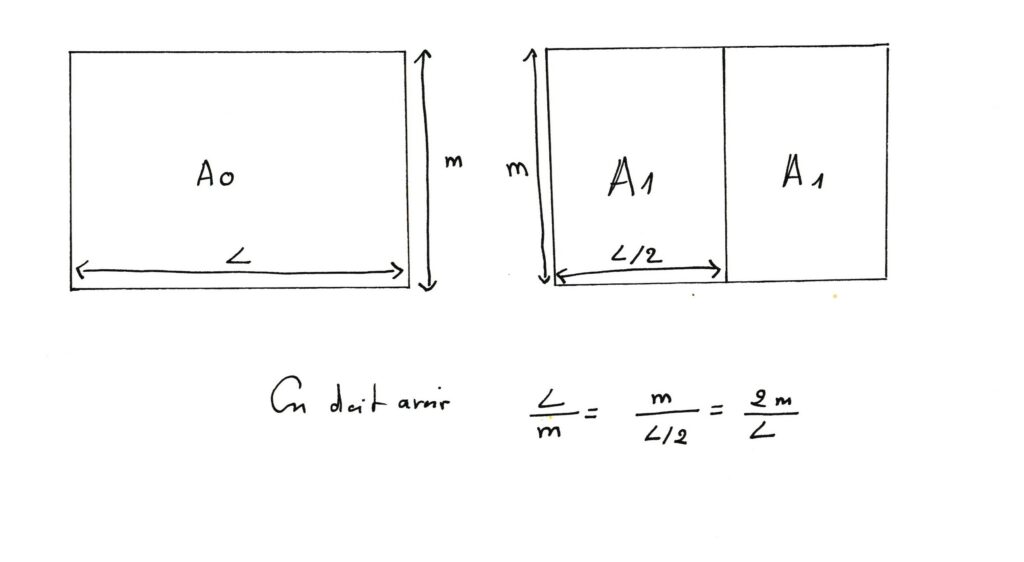
Si L est la longueur et m la largeur de la feuille A0, m est la longueur et L/2 la largeur de la feuille A1. On doit donc avoir L/m=m/(L/2), ce qui donne (L/m)²=2, donc L/m=√2. Or √2 est à peu près égal à 1,41 !
Donc pour qu’à chaque fois qu’on plie une feuille en deux, on obtienne les même proportion, il faut que la dite proportion soit égale à √2.
La feuille A0, doit donc avoir une longueur, L, égale à 1,41 x sa largeur, m. (J’arrondis).
Par ailleurs, afin que ce soit facile de calculer le grammage d’une feuille, on souhaite que la surface de la feuille de départ, A0, soit égale à 1m², soit 10 000 cm².
Or la surface d’un rectangle est égale à largeur x longueur. Ce qui donne pour A0 : (√2 x m) x m = 10 000, d’où m²=10 000/√2 =7071,06. On trouve alors m = √7071,06 =84,09 cm, qu’on arrondit à 84,1 cm. La longueur est alors √2 x 84,1 =118,9 cm (en arrondissant).
Voilà l’explication de ces dimensions pour les feuilles de format A.
En dessous, une vidéo réalisé par Martin Andler, qui reprend ces éléments.
Nombre de pliage d’une feuille
Il est amusant de noter qu’il est impossible de plier une feuille plus de 7 ou 8 fois, peu importe son épaisseur de départ. En effet, en pliant 1 fois, on obtient deux épaisseur, en repliant en deux, on obtient 4 épaisseur. On multiplie par 2 à chaque fois le nombre d’épaisseurs. On appelle cela une suie géométrique.
Au bout de 7 pliages on aura donc 128 épaisseurs, et au bout de 8 pliages, 256. Ce qui rendra impossible de continuer.
Vous trouverez des références ici.
Le nombre d’or
Le nombre d’or est aussi lié à une proportion de rectangle, mais le problème est différent des formats A.
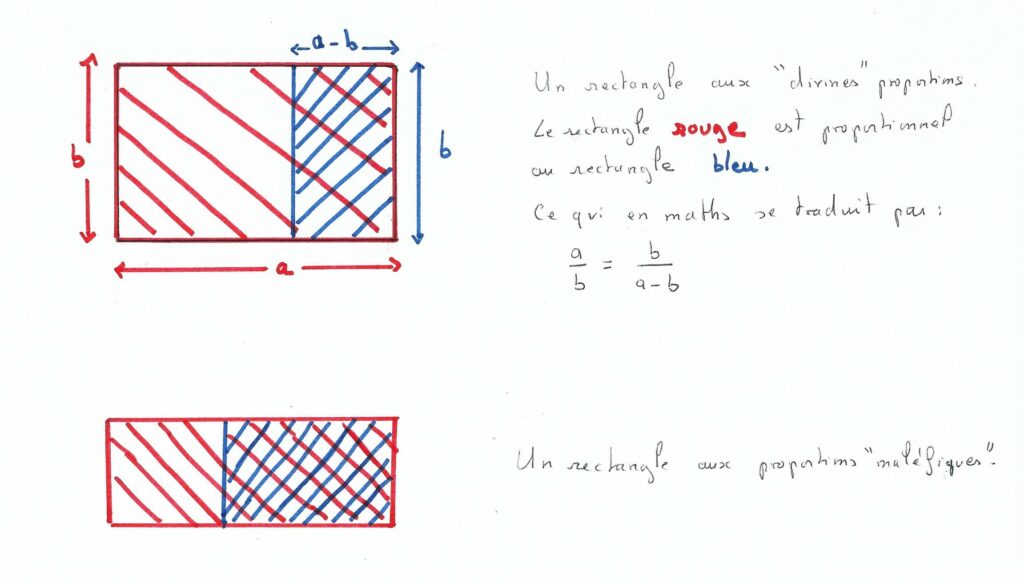
Le nombre d’or est la proportion d’un rectangle, longueur/largeur, ici dans mon dessin a/b, de sorte que le rectangle obtenu en enlevant un carré au rectangle de départ soit dans les mêmes proportions.
Si on note p, cette proportion, on obtient à partir de a/b=b/(a-b), p=1/((a-b)/b)=1/(p-1).
On trouve alors que p vérifie la relation px(p-1)=1, c’est à dire p²-p-1=0.
Cette équation a deux solutions, (1+√5)/2 et (1-√5)/2. On considère la solution positive, ce qui donne la valeur du nombre d’or : (1+√5)/2, qui est à peu près égal à 1,62.
Voici un exemple de construction à la règle et au compas d’un rectangle d’or :
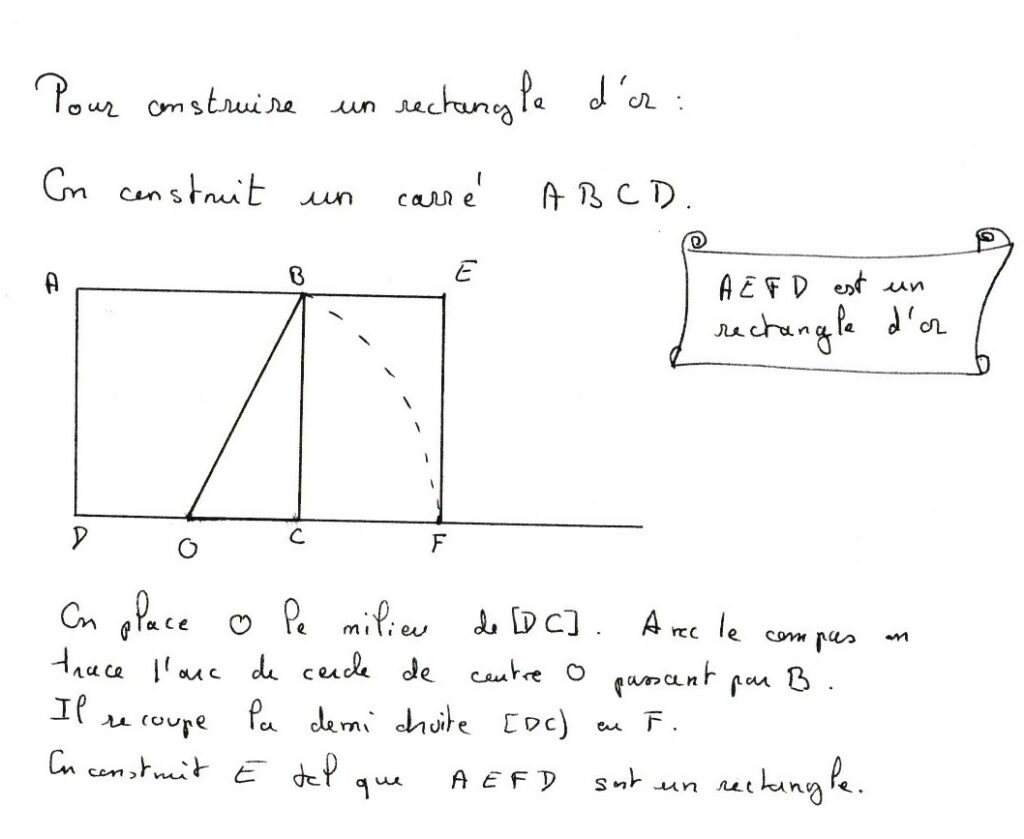
Pourquoi ça marche ? C’est lié au fameux théorème de Pythagore.
Supposons que le carré précédent soit de largeur 1. Le triangle OCB est un triangle rectangle, avec OC=1/2 et BC=1. Le théorème de Pythagore nous dit alors que OB²=OC²+BC²=(1/2)²+1²=1/4+1=5/4.
On obtient alors OB=(√5)/2
La longueur OF est égale à la longueur OB, et la longueur D0 est égale à 1/2. On a donc la longueur DF qui vaut le nombre d’or.