Portrait de François Coquet
J’ai connu François Coquet à l’Ecole Normale Supérieure de Saint-Cloud. Il était en 3ème ou 4ème année quand je suis rentrée à l’Ecole Normale. On s’est peu fréquenté à l’époque, néanmoins, près de trente ans plus tard, je l’ai retrouvé dans une réunion bilan autour des sujets de concours entre professeur d’écoles et professeurs de classes préparatoires. Je ne l’ai pas reconnu tout de suite, ses cheveux ayant blanchis en trente ans, mais sur le chemin du retour, j’ai fait le lien. Depuis, je suis allé visiter l’école dans laquelle il enseigne, l’Ensai, à Rennes, puis nous sommes restés en contact.
François a 55 ans, son parcours scolaire est le parcours classique des gens de sa génération qui étaient « bons partout ». Dans les années soixante-dix, quand on était un bon élève à l’école, on était orienté automatiquement en filière maths, filière C au lycée. Puis, classe préparatoire, maths sup, maths spé. Son premier vrai choix a été dans le choix de l’école intégrée : hors de question de faire l’Ecole Polytechnique – militaire-, hors de question également pour lui de devenir ingénieur. Il a donc choisi d’aller à l’Ecole Normale, qui préparait une carrière de chercheur ou de professeur.
Une fois à l’Ecole Normale, il a préparé l’agrégation de mathématiques « on était là pour ça ». Puis, il a, par hasard, fait un DEA (l’équivalent du M2 actuel) de…probabilité ! Sa compagne habitant à Rennes, il a poursuivi en thèse dans cette ville. Puis c’est (enfin !) posée la question du choix de carrière. Il n’avait pas envie d’être professeur de classes préparatoires, et le milieu universitaire lui plaisait bien, avec ses différentes facettes : recherche, enseignement, administration.
Par chance (encore…) le ministère de l’époque a ouvert des postes, et personne n’était vraiment là pour les prendre (cela ferait rêver les doctorants d’aujourd’hui, ou rager…), il s’est donc retrouvé Maitre de Conférences à l’Université de Rennes, puis Professeur à l’IUT du Havre, avant de revenir à
Rennes en 2005 à l’ENSAI. Parallèlement, de 2013 à 2016 il a été délégué scientifique de l’ AERES (l’Agence de l’Evaluation de la Recherche et de l’Enseignement Supérieur), devenue entretemps HCERES (Haut Comité de l’Evaluation de la Recherche et de l’Enseignement Supérieur).
Quand tu te retournes sur ta carrière, qu’éprouves-tu ? Fierté, satisfaction, regret ?
Je suis étonné. Je n’ai jamais eu de vocation pour les mathématiques. Mais je n’ai aucun regret, j’ai fait des choses qui me plaisaient. Il y a également des tas d’autres possibilités non explorées dans lesquelles je me serais certainement épanoui. Quand je fais le bilan, je me dis que c’est un travail que j’ai beaucoup aimé, et que j’aime encore, dans une certaine mesure.
De quel milieu familial viens-tu ?
Je viens du Havre et je suis un enfant de la classe ouvrière : métallurgie pour la branche paternelle, domesticité pour la branche maternelle. Mes parents sont des purs produits de la méritocratie républicaine : ils sont devenus tous les deux instituteurs. Je suis vraiment le premier de ma famille à être allé aussi loin dans les études. C’était une époque où l’ascenseur social fonctionnait bien. J’imagine que mes parents sont fiers de moi, en tout cas ils m’ont laissé vivre, et ne sont pas intervenus dans mes choix. C’était inutile, de toute façon il y avait une telle pression du système…
Port du Havre
© Tadeáš Skuhra | Dreamstime.com – <a href= »https://fr.dreamstime.com/photos-stockbateaux-dans-le-port-image31945763#res13045069″>Ships in harbour</a>
A l’école tu aimais tout ? Tu étais bon en tout ?
Oui, j’étais assez bon dans les disciplines littéraires que j’aimais beaucoup. J’étais également bon en sciences sociales. Surtout j’étais déjà musicien, je le suis encore. Je sais que c’est un poncif à propos des matheux, ce qui m’agace d’ailleurs. En tout cas j’étais intéressé par énormément de choses et j’aimais bien l’école. C’était gratifiant. J’aime « avaler du savoir ».
Jusqu’au collège, j’étais un OVNI. J’avais un an d’avance, j’étais le premier de la classe, avec tout ce que cela comporte de connotations pénibles. Mais j’ai toujours eu des copains différents. Dans mes bandes, on ne se choisissait pas sur des critères de réussite scolaire ou pas.
Au lycée je n’ai pas eu de problème. Socialement ça se passait très bien, j’étais très à l’aise avec tout le monde. Il se trouvait que, en plus j’étais bon en classe, mais ce n’était pas un problème. Cela vient du fait que je suis d’un milieu où il n’y a pas d’intellectuels. Dans mon milieu familial non plus, ce n’était pas la norme la réussite scolaire.
Quels souvenirs mathématiques as-tu gardé de ta scolarité ?
En CM2, j’ai découvert que l’on pouvait compter dans d’autres bases que la base 10. Cela m’a ouvert à l’idée que le monde pouvait être différent de ce que je connaissais, de ce qu’il paraissait. Je trouvais cela très bien ! On voyait les relations d’ordre, les relations d’équivalence, les ensembles représentés par des « patates ». Tout cela me semblait très simple, limpide. J’ai mis énormément de temps à réaliser qu’autour de moi c’était la panique, y compris chez les professeurs. J’ai fait partie de l’infime minorité pour laquelle ces choses-là semblaient tout à fait naturelles ; en tout cas marrantes. C’est une expérience que tous les mathématiciens de ma génération ont.
Quand est-ce que tu t’en es rendu compte ?
Au début de ma maths sup, au Havre. Le cours commençait par la théorie des ensembles, les applications, les lois de composition, etc. J’étais en fait un des rares élèves à qui tout cela semblait simple. Je me suis dit que je devais avoir la bosse des maths d’une certaine façon, pour arriver sans souffrance à faire ces exercices. Pour moi il s’agissait d’un mécanisme logique, plus ou moins toujours le même, qu’on applique et qui mène au résultat. Quand je disais ça à mes camarades je voyais un voile d’incompréhension dans leurs yeux…
Pourtant ils étaient en maths sup, en classe prépa, ils avaient été déjà triés par le système.
Oui mais c’était vraiment une toute petite maths sup. En deuxième année, j’ai dû aller à Rouen en maths spé, en M’, il n’y en avait pas au Havre. Même là, j’étais encore dans les « bons en maths ». As-tu eu des révélations, des illuminations, liés aux mathématiques ?
Non pas vraiment. Rétrospectivement, j’ai un regard plutôt critique. A l’époque j’ai adhéré à cette espèce de hiérarchie sur ce qui était censé être beau, noble et intéressant en mathématiques : La géométrie, l’algèbre, et un peu en dessous l’analyse et encore en dessous les mathématiques appliquées, un peu sales… Je refusais par principe de faire des mathématiques qui servaient à quelque chose, c’était très couru à l’époque. C’était l’ère de l’intelligence pour l’intelligence, les mathématiques étant l’étalon ultime de l’intelligence humaine ; elles revendiquaient une certaine forme d’inutilité.
Les seuls domaines où je n’étais pas dans les meilleurs, y compris en classe prépa, par snobisme peut-être, c’est quand il y avait du calcul numérique. Il était pour moi hors de question de parler de probabilités, et je détestais le dénombrement… C’est toujours le cas d’ailleurs pour le dénombrement, mais parce que j’y comprends rien…
Rappelle-moi ta spécialité ?
Oui, je sais c’est paradoxal… Dans les études de Licence et Maitrise, j’ai découvert l’aspect mathématiques des probabilités, leur rattachement à la théorie de la mesure et j’ai trouvé cela magnifique. Il n’y avait plus de dénombrement… On voyait l’aspect théorique. Plus tard, je me suis rendu compte quand j’ai commencé à enseigner, qu’on disposait là d’un outil complètement fascinant, qui rendait compte mathématiquement du hasard. Cela me fascine toujours maintenant.
© Igor Terekhin | Dreamstime.com – <a href= »https://fr.dreamstime.com/photo-stockmatrices-image53264939#res13045069″>Gambling. Dice.</a>
Pourquoi as-tu choisi de faire des probabilités ta spécialité ?
Après l’agrégation, j’ai voulu faire un DEA. A l’époque j’étais objecteur de conscience, je travaillais à Paris auprès d’aveugles. Il me fallait faire quelque chose avec le moins d’heures de présence possible et également situé pas trop loin de là où résidait ma compagne, à Saint-Cloud. J’ai mis en œuvre un espèce d’algorithme d’optimisation logistique, le DEA de probabilité de Paris 6 était la meilleure option.
On peut voir cela comme une utilisation des mathématiques dans la vie courante. Je ne regrette pas du tout ce choix. J’ai bien aimé les mathématiques utilisées en probabilités et en plus, le fait que ça parle de choses « vraies » c’est devenu vraiment important pour moi. Les phénomènes liés au hasard, je continue de les trouver fascinants. Il y a plein de paradoxes. Le plus beau paradoxe étant peut-être la loi des grands nombres, qui dit que, quand on lance un grand nombre de fois une pièce, on va obtenir en gros autant de « face » que de « pile », alors que, à chaque fois qu’on lance la pièce, on rajoute du hasard. Enfin on croit qu’on rajoute du hasard, mais en fait on en élimine. C’est une loi, comme la loi de la gravitation, c’est expérimental et c’est inexorable. Et en plus c’est un théorème. C’est démontré.
Est-ce qu’on n’a pas inventé les mathématiques qui vont bien pour le démontrer ?
Non, il y a trois siècles entre Bernoulli qui a énoncé cette loi et Kolmogorov qui l’a démontrée sous sa forme générale dans les années 30 du 20ème siècle, ce n’est pas si vieux que ça. Entre temps l’idée de formaliser une probabilité a vu le jour et on s’est rendu compte qu’on arrivait à étendre ce théorème pour l’avoir dans une forme a peu près stable. Ce phénomène-là s’observe également avec son petit frère, le théorème de la limite centrée. S’il y a un truc qui me restera de ma vie de matheux ce sera ça.
Et le théorème de Pythagore.
Pourquoi Pythagore ?
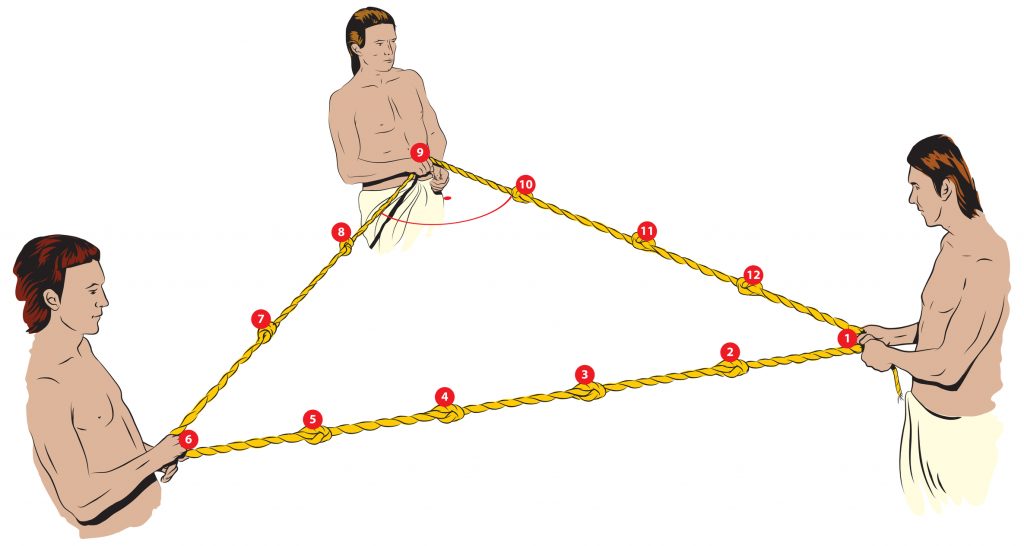
D’abord, il a quelque chose d’universel, tout le monde s’en sert, « dans la vraie vie ». Par exemple, ma fille qui est régisseuse plateau, s’en sert tous les jours. Tous ceux qui ont à faire de l’architecture connaissent la règle du 3-4 -5, pour vérifier qu’un angle est droit.
Pour s’assurer qu’un angle est droit : 3²+4²=5²
© Lukaves | Dreamstime.com – <a href= »https://fr.dreamstime.com/illustration-stock-corde-degyptiens-image53764606#res13045069″>Egyptians rope</a>
De plus, le théorème de Pythagore on le retrouve dans des mathématiques beaucoup plus techniques. En statistiques par exemple, dans les modèles de régression : en gros il s’agit de trouver la droite qui approche « le mieux » un nuage de points et la théorie repose en grande partie sur le théorème de Pythagore. Quand j’enseigne à des « bacs plus quatre » cette théorie, je leur démontre de belles propriétés de l’estimateur des moindres carrés ordinaires, et je leur dis « là, ce dont on a besoin c’est du théorème de Pythagore ». Il faut que je passe trois-quatre minutes pour qu’ils le reconnaissent parce que c’est noyé dans des trucs beaucoup plus formalisés, compliqués.
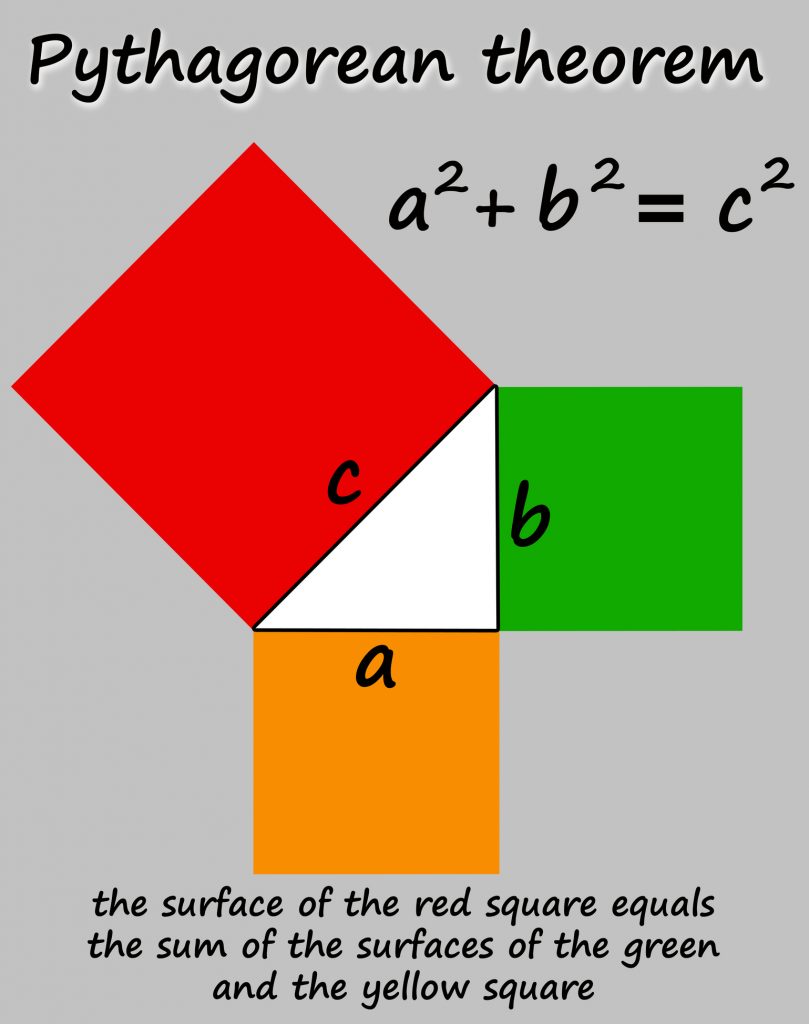
Le théorème de Pythagore en anglais
© Alain Lacroix | Dreamstime.com – <a href= »https://fr.dreamstime.com/image-stockmathmatiques-image26301601#res13045069″>Mathematics</a>
Et quelles sont les mathématiciens chers à ton cœur ?
Je t’avoue que cette question m’a posé un gros problème. Je ne suis pas du tout fétichiste. C’est mon côté distancié par rapport aux mathématiques sans doute. J’ai pensé aux « tartes à la crème », Galois, Grothendieck… Mais il y a quelqu’un auquel je pense particulièrement, c’est Cédric Villani.
Cédric Villani possède à peu de choses près tout pour m’horripiler. Le côté star médiatique. Cependant je suis obligé de reconnaitre deux choses. Je l’ai souvent lu et entendu, et ce qu’il dit me semble généralement très pertinent. Il est tout à fait capable de faire la part en lui du professeur, du chercheur, et je respecte ce qu’il écrit.
Il se trouve que dans mes fonctions d’évaluateur, j’ai eu à évaluer son laboratoire, l’Institut Camille Jordan à Lyon. Pour tout le comité d’évaluation la question qui se posait c’était « est-ce que la star Villani va venir pendant la visite du comité ? », visite qui a duré trois jours, c’est un très gros laboratoire. Le premier jour avec « les grandes messes », pas de Villani. Mais au moment où l’on a un entretien spécifiquement avec son équipe, il est venu, il était avec son équipe. Il ne l’a pas joué plus modeste que ça, mais il l’a fait, il était là.
C’est quelqu’un de vraiment respectable en fait.
Il a dit récemment à la radio (sur France Inter), que les statistiques c’était du mensonge, en citant Churchill : « il y a les mensonges, les très gros mensonges et les statistiques ». Ça m’a déçue, je ne pense pas que les statistiques mentent, c’est éventuellement l’usage que les non-mathématiciens en font qui est discutable. Tu en penses quoi, toi le spécialiste ?
En effet, il faut une très grosse technicité pour faire des statistiques, technicité que la plupart des gens n’ont pas. Il faudrait se départir de la magie des chiffres. Comprendre à quoi servent réellement les statistiques, la notion de risque d’erreur. En fait, il s’agit d’une aide à la décision. Il y a une marge d’erreur, parce qu’il y a du hasard qui peut faire que les choses ne se passent pas comme on s’y attend… C’est dangereux, il faut rester lucide, ne pas jouer sa vie sur un coup de dé.
Les statistiques ne donnent pas de réponse sur le destin individuel (par exemple ce n’est pas parce qu’on est dans un lycée ayant un gros pourcentage d’admis à l’Ecole Polytechnique qu’on va forcément y rentrer…), mais décrivent le comportement une cohorte.
Oui, en fait, il y a des biais. Qu’est-ce qu’on échantillonne et comment on choisit « l’échantillon représentatif ». A l’époque des big data, c’est un immense enjeu de société. La donnée chiffrée ne dispense pas d’être intelligent. C’est ce qu’il faut expliquer en statistiques.
L’exemple le plus célèbre c’est la réélection de Roosevelt aux Etats-Unis en 1936. Un journal avait fait un énorme sondage, sur un million et demi de personnes, qui donnait gagnant de manière écrasante son adversaire. C’est à cette occasion que George Gallup (celui du célèbre institut), a publié sa première étude sur 3600 personnes. Il a prévu que Roosevelt allait battre son opposant à plate couture. Ce qui s’est passé, c’est que le journal, qui était républicain, a fait son sondage parmi ses abonnés, ceux qui avaient le téléphone et une voiture. La représentativité de l’échantillon des personnes interrogées n’était pas bonne.
Si on regarde la chance de réussir en classe préparatoire, il faut se demander d’où viennent les gens qui la composent. En d’autres termes, quelle est la valeur ajoutée du lycée. Evidemment il y a un taux de réussite plus élevé au lycée Henri IV, mais qui rentre à Henri IV? Si un élève rentre à Henri IV cela veut déjà dire qu’il a plus de chance de réussir, au départ. Ce n’est pas le passage par le lycée qui compte. Ce sont typiquement des choses très difficiles à expliquer. Tous les jours à la radio, à la télévision, dans les médias, on sort des statistiques faussées. Pour commencer on ne donne pas la part de risque.
Comment expliques-tu le résultat des élections américaines, la victoire « imprévue » de Donald Trump, et peu de temps après, la surprise de l’élection de François Fillon à la primaire de droite ?
La question des sondages, en effet d’actualité, est complexe. En fait, les sondages d’opinions électoraux sont très spécifiques, à peu près ignorés par la statistique publique (Ined, Insee…) et sont faits paradoxalement avec une méthodologie statistique très faible. Les instituts de sondages emploient très peu de statisticiens (sauf Mediametrie), et en général pas pour les sondages électoraux.
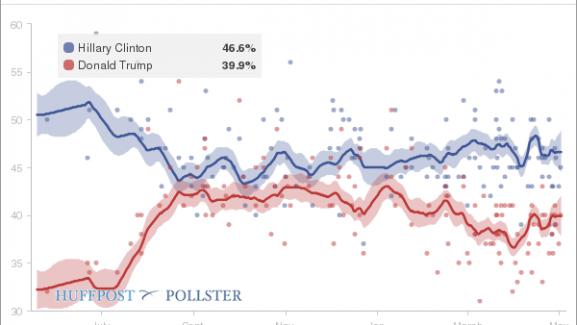
Evolution des intentions de vote en faveur de Donald Trump et Hillary Clinton d’après les moyennes des sondages effectués entre mai 2015 et mai 2016. (HUFFINGTON POST / POLLSTER)
Parmi tous les problèmes méthodologiques, il y a la fonction du sondage : est-il descriptif ou prédictif, est-ce une estimation ou un test « qui va gagner ? ». Il faut également prendre en compte la volatilité de l’opinion et la sincérité des répondants, les micro-différences entre les questions posées qui peuvent aboutir à des réponses apparaissant comme paradoxales si on ne les analyse pas à un niveau fin, ce qui n’est pratiquement jamais le cas. Le fait aussi qu’une réponse chiffrée correcte peut aller de pair avec un résultat contre-intuitif (dans le cas des Etats-Unis, Hillary Clinton l’emporte nettement en termes de voix, mais perd en termes de grands électeurs, et je ne me rappelle pas d’avoir entendu parler avant l’élection de beaucoup de sondages sur le nombre de grands électeurs obtenus par chaque candidat). Ajoute à cela une certaine méconnaissance de la base de sondage, c’est-à-dire des votants (flagrante dans le cas de la primaire de la droite…)
Le point le plus important reste qu’on ne devrait jamais donner des réponses en termes de points, mais en termes d’intervalles de confiance, avec un calcul de marge d’erreur prenant en compte toutes les incertitudes liées aux points ci-dessus. Chose qu’on sait à peu près faire pour les sondages sur des données objectives (conditions de vie des ménages, etc…), mais c’est beaucoup plus délicat pour les sondages d’opinion. Les marges qu’on obtient quand on essaie de calculer la précision en prenant en compte toutes les incertitudes, sont trop pessimistes pour être vendues, et pour être franc, je pense qu’elles sont trop pessimistes tout court…
En gros, ce qu’on sait à peu près faire statistiquement, c’est du sondage « sortie des urnes » où là on retrouve du fait objectif, et on ne se trompe guère.
Dans une moindre mesure on est capable de faire des sondages sur des scrutins proportionnels, type élections européennes, où les chiffres qu’on est capable de mesurer répondent à la vraie question posée (quel score pour telle liste ?) et non à des questions implicites beaucoup plus délicates (qui gagne ? combien de députés/grands électeurs ? ). Mais en matière de prédiction, il faudrait pouvoir tenir compte des éventuelles dynamiques, des incidents de parcours entre la date du sondage et celle de l’élection, etc…
Enfin, comme indiqué plus haut, à de rares mais notables exceptions près (Médiamétrie), les instituts de sondages ne sont pas le débouché naturel de nos élèves…
Que représentent les mathématiques pour toi ?
Je ne suis pas passionné par les mathématiques en fait. Certes, j’y ai consacré pas mal de mon temps. Pour moi, c’est un métier, que j’exerce, et c’est loin d’être le pire. Mais je n’ai jamais choisi de faire des mathématiques.
Qu’aurais-tu aimé choisir alors ?
Ma passion évidente c’est la musique, c’est clair. Il ne s’agit pas du côté tarte à la crème des matheux musiciens, ce qui m’horripile. Parce que moi, je dissocie complétement les deux : la musique et les mathématiques. Néanmoins, il a fallu que j’y réfléchisse : pourquoi ce poncif ? Je pense, même si ça me coûte de le reconnaitre, qu’il y a des choses communes dans ces deux objets : un certain goût pour l’abstrait (il s’agit à chaque fois d’un langage) et le sens de la construction formelle. La plupart des matheux qui aiment la musique mettent Bach au-dessus de tout. C’est très symptomatique.
Le truc, c’est que moi je ne le vis pas du tout ça comme ça. Les mathématiques pour moi c’est purement intellectuel, alors la musique c’est purement physique. Je ne fais pas de lien entre les deux.
Je fais de la musique essentiellement contemporaine. Je suis spécialisé dans la musique savante du 20-21 siècle, des compositeurs vivants, dans la musique expérimentale. En même temps ces expériences datent d’il y a 50 ans, on pourrait peut-être arrêter de l’appeler comme ça. A notre époque on peut faire le tri entre les expériences : celles qui ont sombré dans l’oubli et les autres, et employer une autre terminologie.
Je suis saxophoniste. Ce que je joue est très varié. Il y a des choses extrêmement écrites, d’autres comportant de grandes plages de liberté. On a remis en cause toutes les conceptions acquises du vrai, du beau. Rien n’est nécessairement ni beau ni laid en soi. Ceci est très accepté dans le jazz. Mais c’est plus difficile dans le cas de la musique savante. Face à une musique nouvelle, c’est mieux de l’aborder avec des oreilles ouvertes. Chercher ce qu’elle veut nous dire et ne pas réagir par comparaison avec un catalogue de « ce qui est beau ». Je suis très attaché à ça. J’ai utilisé tout ce que j’ai appris pour faire de l’improvisation collective, avec des danseuses, pour faire des choses très différentes. J’ai eu une activité semi professionnelle jusqu’à quarante ans : je ne jouais qu’avec des musiciens professionnels.
Pourquoi n’es-tu pas devenu musicien professionnel ?
La question s’est posée quand j’avais vingt-quatre, vingt-cinq ans. Mes camarades professionnels m’ont dit : « tu n’as pas besoin de ça pour gagner ta vie. Si tu es motivé, tu vas pouvoir garder ce qui est bon (jouer) et ne pas galérer (être professeur de musique par exemple…), tu as déjà un boulot ». Et accessoirement je ne faisais pas de concurrence déloyale à ceux qui n’avaient pas le choix…
J’ai une très bonne gestion de mon temps. Je cloisonne énormément, ce qui me fait gagner du temps. J’ai donc pu effectivement mener ces deux activités exigeantes de front. Mais vers mes quarante ans, j’ai levé le pied. J’ai eu la peur du concert de trop. De me rendre compte que je n’assure plus.
Maintenant cela m’est égal. Si je fais le concert de trop tant pis, j’aurais fait tous les autres avant.
Tu t’amuses.
C’est beaucoup plus que de l’amusement. C’est beaucoup plus fort. Il y a des enjeux là-dedans existentiels. Quand je joue, quand je suis dans le processus de préparer un concert, ce sont les moments les plus précieux de mon existence… Tu n’as pas idée des enjeux que je mets là-dedans.
J’ai un refus clair de concilier les deux (mathématiques et musique). Plus jeune j’ai hésité un moment à aller voir à l’Ircam, avec cette double casquette. Mais finalement non, je ne veux pas mélanger. Parce que je pense que ça s’adresse à deux parties complètement dissociées de ma personnalité.
Les mathématiques c’est une activité professionnelle, intellectuelle, que j’arrêterai sans problème l’heure venue. Je ne fais pas de mathématiques en dehors de mon travail.
La musique je le ressens comme complètement physique, je n’arrêterais jamais. J’écoute aussi énormément de musique ; j’ai d’abord un rapport physique à la musique que j’écoute.
Eventuellement après, je regarde comment elle est construite. Par contre, je m’écoute très peu. Il y a très peu de traces de ce que j’ai fait. Je ne m’enregistre pas.
Une vidéo trouvée sur le net : https://vimeo.com/28824366
https://www.le–terrier.net/albums/poesiesonore/11.htm
https://www.le–terrier.net/albums/poesiesonore/sons/donner_le_ton.mp3
Quelle place tient l’enseignement dans ta vie ?
Une place extrêmement importante. Je n’avais pas la vocation. Mais elle m’est venue quand je me suis retrouvé devant des élèves. Je me suis aussi posé beaucoup de questions, sur notre utilité sociale en tant que professeur de mathématiques. En tant que chercheur c’est plus simple. Pendant un ou deux ans, j’ai cru que si pour certains les mathématiques étaient difficiles ou incomprises, c’était parce qu’ils n’avaient pas rencontré les bons professeurs. Mais je me suis rendu compte que non, ça ne marche pas comme ça. Il y a des gens qui n’aiment pas, qui n’ont pas envie, qui ne sont pas doués. Pourquoi alors leur fait-on faire autant de mathématiques ? Il y a eu un traumatisme dans la communauté des professeurs de mathématiques à l’époque où Claude Allègre était ministre de l’Education Nationale. Il a fait tomber les mathématiques de leur piédestal. A l’époque, bien que j’ai participé à la détestation de Claude Allègre, j’ai trouvé que la réponse de la communauté était extrêmement décevante, voire faible. Le problème chez les professeurs de mathématiques c’est qu’ils n’avaient pas beaucoup de réponses à la réflexion « ce que vous faites ça ne sert à rien », à part « c’est beau, et c’est indispensable à tout le monde ». Comme tout cela faisait écho à pas mal de questions que je me posais, je me suis intéressé à trouver des réponses et je me suis spécialisé dans « enseigner les maths pour les non spécialistes ». Je me suis désintéressé de la « reproduction de l’espèce » (enseigner les mathématiques à des futurs professeurs de mathématiques qui formeraient à leur tour de nouveaux professeurs, etc.) et j’ai enseigné les mathématiques pour les biologistes, les économistes, les informaticiens, en adoptant la démarche suivante : j’allais d’abord discuter avec les spécialistes de ces cursus-là pour savoir de quelles mathématiques ils avaient besoin. Ensuite je voulais arriver à les convaincre que c’était mieux que ce soit fait par un mathématicien, qui allait faire des mathématiques rigoureuses, qui ne trichent pas, et iraient au but qu’ils attendaient. C’était plus compliqué à faire passer. Ils étaient tous convaincus qu’ils avaient besoin de mathématiques, mais pas de matheux…
Voici l’exemple dont je suis le plus content. J’ai participé à l’élaboration d’une réforme pour maintenir des mathématiques dans un cursus de biologie. J’avais eu accès aux données de Mendel, les petits pois, la génétique etc. J’ai proposé un cours de mathématiques construit de la manière suivante : partir des chiffres des expériences de Mendel sur les petits pois. Au bout de deux générations par la méthode des croisements il y avait par exemple 713 petits pois lisses et 239 petits pois fripés. Une proportion un quart/trois quart, quasiment. Il en a déduit les « lois de Mendel ». Tout est dans le « quasiment ». J’ai axé mon cours sur la question suivante : scientifiquement, Mendel avait-il le droit de faire cette approximation ?
J’ai demandé aux professeurs de biologie s’ils étaient capables de répondre à cette question. Bien sûr que non, ils n’en étaient pas capables. Parce que pour répondre à cette question, il faut des mathématiques, et probablement des matheux. J’ai bâti à l’époque tout mon cours de « proba stats » avec ça comme fil rouge, pour arriver à la réponse à la fin, et que non, on n’arrive jamais exactement sur un quart/ trois quart. Voilà. Au moins j’y trouvais une espèce d’utilité sociale. Cela montrait que les mathématiques sont utiles.
Par la suite, J’ai préféré faire les mathématiques utiles aux biologistes, informaticiens, etc., même si ce n’était pas « mes » mathématiques.
Tu disais que quand tu étais jeune tu étais « maths pures » à fond, c’est une complète révolution.
Oui, c’est une évolution- révolution, progressive mais assez rapide quand même. Et sans par ailleurs critiquer ceux qui font des mathématiques pures. Mais moi je ne vivais plus bien là-dedans.
Les statistiques, on ne les fait jamais pour le plaisir, on fait ça parce que ça sert, pour répondre à des problèmes posés par les médecins, les banquiers, les politiques, les « marketteurs », etc. Je suis satisfait d’avoir la capacité de comprendre de quelles mathématiques les gens ont besoin.
Tu dirais quoi à un jeune à qui ne comprend pas pourquoi on le force à faire des mathématiques ?
L’enseignement au collège ne doit pas être utilitaire. Il s’agit de bâtir un socle commun, d’avoir une culture commune. Les mathématiques font parties de la culture. De plus, si les collégiens veulent pouvoir progresser dans d’autres filières, ils doivent savoir un peu plus que simplement compter. Je pense par ailleurs que le côté maniement de l’abstraction c’est une bonne formation de l’être humain.
Et au lycée ?
De l’extérieur, je me dis si j’étais professeur de lycée je m’éclaterais dans les TPE, dans l’idée que sur un sujet donné on va faire travailler en interaction plusieurs disciplines. J’apprécie beaucoup l’enseignement par projet. J’aurais aimé que cela existe à mon époque.
Est-ce que tu as des choses à rajouter ?
Il y a dans ma carrière deux aspects qu’on n’a pas encore évoqués : chercheur et évaluateur.
Chercheur, ça m’a vraiment intéressé. J’ai eu quelques moments forts : j’ai vu des mathématiques se créer, j’y ai contribué. Intellectuellement, c’est gratifiant. J’ai travaillé avec des gens extrêmement forts qui avaient en tête des résultats bien avant que les concepts soient créés et mis en équation. J’ai vécu quelques belles illuminations, qui resteront parmi les bons souvenirs de ce métier. Par exemple, j’ai participé à l’élaboration d’un nouveau concept, les martingales non linéaires, qui vit maintenant, qui existe. Un autre concept dont je suis fier, mais qui n’a pas vécu : la convergence des filtrations. En tout cas, quand on arrive à créer un concept mathématique qui manque, c’est vraiment chouette.
En tant qu’évaluateur AERES, j’ai visité plus de la moitié des laboratoires de mathématiques de France. Curieusement ça m’a beaucoup réconcilié avec la communauté. Dans la plupart des laboratoires les gens faisaient plutôt bien leur boulot, ils essayent de se poser des questions. J’avais une image négative de la communauté depuis ma déception quant à l’absence de réponse sur l’utilité sociale des mathématiques, suite aux attaques de Claude Allègre quand il était Ministre de l’Education Nationale fin des années 1990. Beaucoup de chemin a été parcouru depuis. En partie à cause des problèmes posés par la pénurie d’étudiants scientifiques. Les mathématiciens sont restés dans leur tour d’ivoire pendant trop longtemps, vivant le reste du monde come un peu hostile. Ils en sortent maintenant et c’est bien. Les mathématiciens tissent des liens avec les autres disciplines et c’est profitable, y compris pour les « maths pures ».
Tous les champs de la société ont besoin des mathématiques, à un moment ou à un autre. Et pour cela, pas besoin d’être « programmé » pour faire des mathématiques dès le plus jeune âge ! On ne le dit pas assez, même en commençant tard on peut faire des choses techniquement impressionnantes. Je le vois régulièrement dans mon école, l’ENSAI, où des étudiants venant de série ES ou même L se débrouillent très bien en mathématiques. Il faut désacraliser les mathématiques, en amont et en aval. Il est tout à fait possible de faire des mathématiques sans être passé par la « voie royale ». On peut très bien proposer des mathématiques pour répondre aux besoins d’autres communautés. J’aimerais que les mathématiques soient une activité de l’esprit parmi les autres, même s’il est important aussi que les mathématiques continuent à se développer pour elles-mêmes. C’est quand même la chose à laquelle je crois le plus. Si je continue à aimer les mathématiques, c’est vraiment pour ça.