Inspiré de Stanislas Dehaene, dont on trouvera la conférence au Collège de France ci-dessous.
https://www.youtube.com/watch?v=rOFxexbfX04
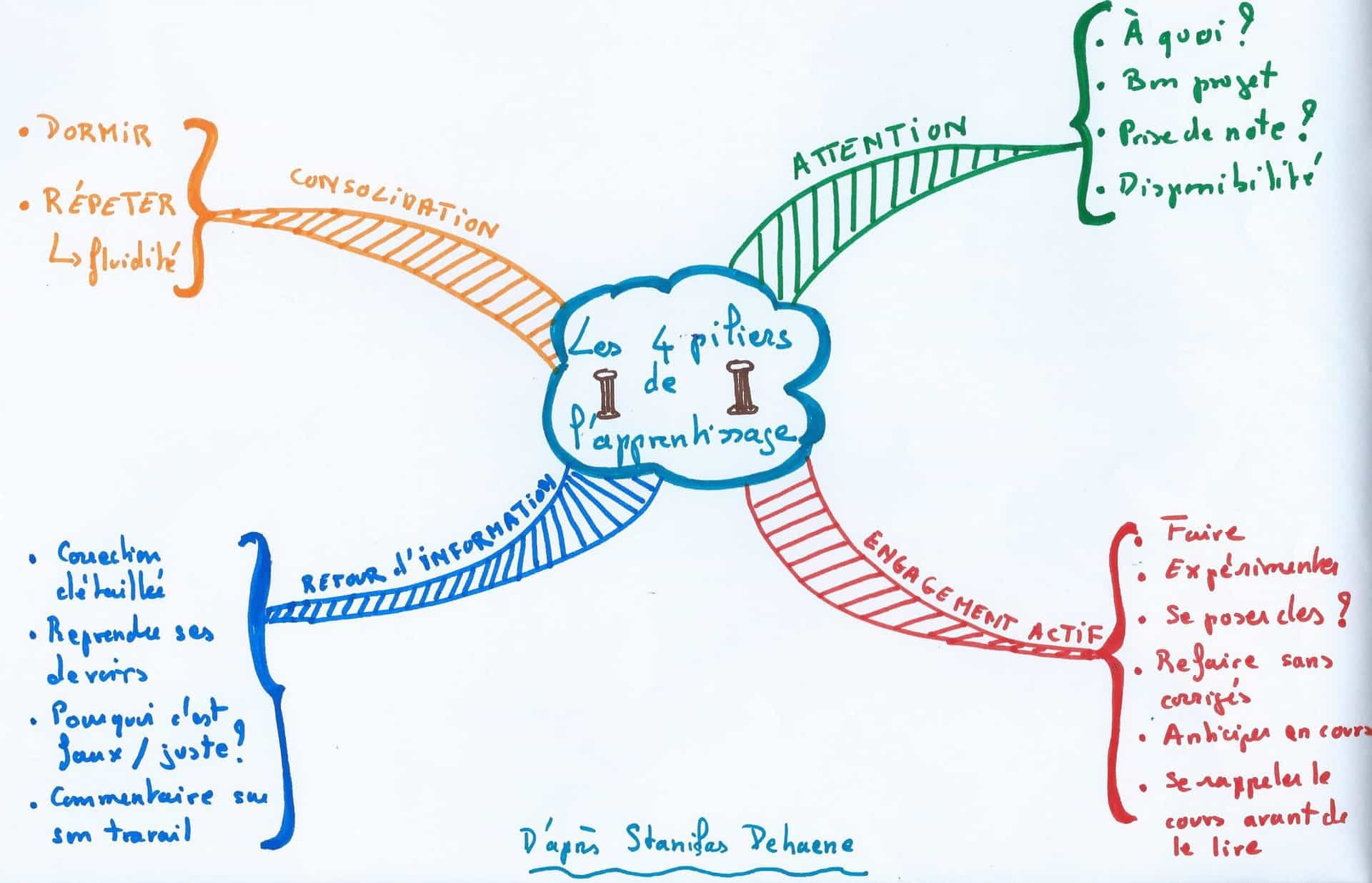
Les quatre piliers de l’apprentissage sont l’attention, l’engagement actif, le retour d’information et la consolidation.
Je les décline ici dans le cadre scolaire, en particulier concernant les mathématiques.
Attention
Il s’agit d’abord de faire attention en cours. Bien sûr, mais attention à quoi ? Attention à ce que dit le professeur, pas uniquement à ce qu’il écrit. Prendre des notes peut aider à la concentration, bien sûr, mais il est important de prêter attention à la structure du raisonnement, aux idées exposées (par exemple inutile de noter toutes les étapes d’un calcul, mais plutôt des indications -factoriser, dériver, faire un changement d’indices etc.- et le résultat final, afin de pouvoir refaire le calcul et se vérifier). Chercher à se faire une représentation personnelle des concepts, en s’appuyant en particulier sur le vocabulaire (les nombres complexes: ce sont d’abord des nombres, en quoi sont-ils complexes?)
Quand on entre dans la salle de classe, il faut avoir le bon projet. Celui de se remplir, de connaissances, de méthodes, d’idées. Celui de réutiliser ses connaissances. Celui de participer, voire d’anticiper sur ce que va dire le professeur.
Pour pouvoir être attentif et concentré, il faut être disponible. Si on est fatigué, stressé ou sous le coup d’une émotion (colère, peur, joie ou tristesse) ce sera difficile. Il faut d’abord régler ce problème. Voir mon article précédent sur l’accueil des émotions.
Le retour d’information
C’est avoir un retour sur ce qu’on fait : le raisonnement est-il correct ou pas, et pourquoi. Même si c’est un moment souvent désagréable, passer au tableau pour résoudre un exercice est intéressant: on a un retour immédiat du professeur (bon, ok, parfois c’est un peu violent !)![]()
A ce sujet, il est important de noter l’importance des erreurs, trop souvent évacuées de l’enseignement : le cerveau procède par ajustement, les erreurs et le retour sur les erreurs, la compréhension de ses erreurs, permettent de se corriger, de réajuster. Il ne faut pas craindre de faire des erreurs. Ce qu’il faut craindre, c’est de ne rien en faire, et de recommencer. Bien sûr ce n’est pas agréable de faire des erreurs, c’est très inconfortable. Il faut se retenir de l’effacer, de gommer, et c’est bien d’y revenir et de comprendre à quel moment le raisonnement s’est fourvoyé. En particulier, souvent les élèves ayant eu des mauvaises notes mettent leur copie au rebut, sans même les relire. C’est dommage. C’est en refaisant le problème, correctement, que l’on progresse. D’abord, c’est satisfaisant de réussir (même si ce n’est plus noté), mais en plus, et surtout, il faut comprendre ce qui s’est passé: est-ce qu’on avait mal appris le cours, pourquopi on n’a pas pensé à utiliser tel ou tel théorème, quels indices dans l’énoncé nous y ferons penser la prochaine fois, est-ce qu’il y a quelque chose qu’on n’a pas compris, quoi?….). Ne pas évacuer non plus les erreurs de calcul en les qualifiant « d’erreurs d’étourderies »… Derrière une erreur d’étourderie, il y a toujours un vrai problème: soit une règle est mal comprise, soit on fait plusieurs choses à la fois, soit on s’organise mal dans son calcul. Est-ce qu’on fait des « erreurs d’étourderies » quand on conduit? Quand on suit un chemin pour aller chez un ami? Quand on joue à un jeu vidéo?
Engagement actif
Pour apprendre, il faut être engagé activement. Assez rapidement il faut faire. On peut regarder pendant mille heures un skieur dévaler des pistes aux jeux olympiques, la seule façon d’apprendre vraiment à skier c’est de monter sur des skis et d’aller soi-même sur les pistes !
Il faut veiller également à ne pas être en pilote automatique en cours. Souvent, en classes préparatoires, le rythme étant très soutenu, les élèves se retrouvent à noter tout ce qu’il y a au tableau, sans comprendre, de peur de manquer une information capitale, sans écouter le prof qui parle déjà sur le tableau suivant. Dans ce cas-là, il faut peut-être se demander l’utilité de la prise de notes ? Il est certainement plus utile, au lieu de noter une démonstration, ou de prendre un corrigé, d’essayer d’anticiper ce qu’il faut faire (on retrouve partout, en des milliers d’exemplaires, les démonstrations). Ou bien de chercher à noter quelques mots-clés, les idées utilisées. Se poser des questions : quels indices dans l’énoncé ont fait penser à tel ou tel théorème, est-ce qu’il y a une autre façon de faire, est-ce qu’on a bien utilisé toutes les hypothèses, etc.?
Chez soi, au lieu de faire des exercices, en regardant le corrigé, essayer d’inventer des énoncés d’exercices, en prenant modèle sur un exercice du cours.
Consolidation
Et pour finir, il faut consolider ce qu’on a appris.
Pour cela, deux choses sont importantes :
le sommeil, car c’est pendant les phases de sommeil que le cerveau « trie et range » les informations. Bon nombre d’élèves en préparation de concours ou d’examens prennent sur leur sommeil. Or sans un sommeil suffisant, il est impossible de réfléchir correctement. On n’arrive pas à accéder à ses connaissances et plus rien « ne rentre » dans le cerveau. Au lieu de se culpabiliser en allant se coucher, on peut se dire qu’au contraire, c’est là qu’on travaille le plus!
La répétition est également fondamentale. Refaire plusieurs fois le même exercice, en approfondissant à chaque fois (attention à ne pas le faire de mémoire). S’entraîner également au calcul. Jusqu’à ce que cela devienne fluide.